Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 97

97- A cabine e a unidade motora da pá carregadeira articulada mostrada na figura estão ligadas por um pino vertical localizado 2   m atrás das rodas da cabine. A distância de C para D é 1   m . O centro de gravidade da unidade motora de 300   k N está localizada em G m enquanto que os centros de gravidade da cabine de 100   k N e da carga de 75   k N estão localizados em G m e G l , respectivamente. Sabendo que a máquina está em repouso e com os freios soltos, determine a ) as reações em cada uma das quatro rodas b ) as forças exercidas pela unidade motora em C e D .

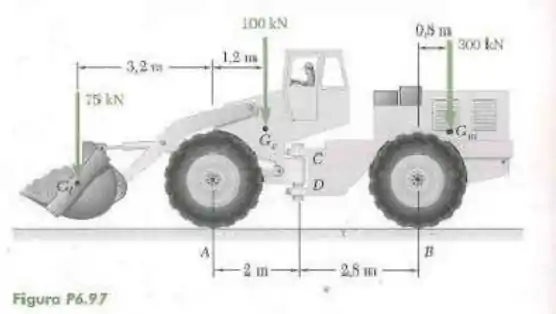
Passo 1

Começando pela análise das forças no corpo todo nós temos a seguinte distribuição de forças.

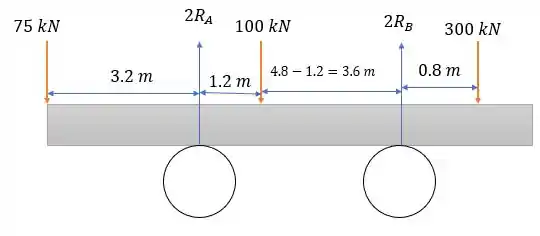
Não esquecendo que temos dois pneus em A e dois pneus em B . Fazendo a somatória dos momentos em A nós teremos:

75 × 3.2 - 100 × 1.2 + 2 R B × 3.6 + 1.2 - 300 × 1.2 + 3.6 + 0.8 = 0

- 1560 + 9.6 R B = 0 → R B = 162.5   k N

E pela somatória das forças verticais temos:

2 R A + 2 R B = 75 + 100 + 300

R A = 75   k N

Passo 2

O pino junta os dois corpos imprimindo forças horizontais em C e em D , considerando o corpo da direita como o nosso objeto de estudo, nós teremos então o seguinte diagrama de forças.

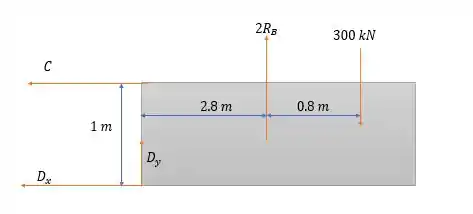
Temos que considerar um D y (senão o pino cai hahah)

Fazendo a somatória dos momentos em C nós teremos:

- D × 1 + 2 R B × 2.8 - 300 k N × 2.8 + 0.8 = 0

D x = 2 × 162.5 k N × 2.8 - 300 k N × 3.6 = - 170   k N

Logo pela somatória das forças horizontais nós teremos:

C = 170   k N

E pela somatória das forças verticais temos que:

D y - 300 k N + 2 × 162.5   k N = 0 → D y = - 25   k N

Logo a reação em D vale:

D = - 25   k N j + - 170   k N i

Resposta

a )   R A = 75   k N ; R B = 162.5   k N

b )   C = 170   k N i ; D = - 170   N i - 25   k N j

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

26. Uma haste de um quarto de círculo de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 30 ° .
27. Para a haste do problema 7.25 , determine a intensidade e a localização do momento fletor máximo:
28. Para a haste do problema 7.26 , determine a intensidade e a localização do momento fletor máximo:
Oito placas retangulares idênticas de 500 × 750m m , cada qual com massa m = 40k g são mantidas em um plano vertical como mostram as figuras. Todos os apoios consistem em planos sem atrito, roletes ou
Um cursos B de peso W pode mover-se livremente ao longo da haste vertical mostrada na figura. A constante de mola é k , e a mola não fica deformada quando θ = 0 . ( a ) Deduza uma equação em função de