Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 30
Um colar C de kg desliza sobre uma barra horizontal entre as molas A e B. Se o colar é empurrado para a direita até que a mola B seja comprimida mm e em seguida liberada, determine a distância que o colar percorrerá, admitindo (a) que não haja atrito entre o colar e a barra, (b) um coeficiente de atrito.
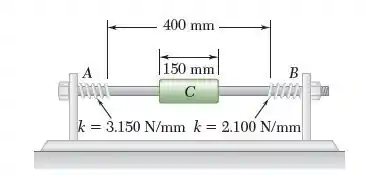
Passo 1
E aê!?! Tudo blz? Neste exercício devemos calcular (item a) a distância que o colar percorrerá, sem atrito, e (item b) com um coeficiente de atrito.
(a)
Distância total
(b) Agora assumiremos que o colar C não atinge a mola em B, devido ao atrito.
Resposta
(a)
(b)
Exercícios de Livros Relacionados
O setor e as rodas vinculadas são liberados a partir do repouso na posição mostrada no plano vertical. Cada roda é um disco circular maciço com uma massa 5 k g e rola sobre a trajetória circular fixa
O braço uniforme O A tem uma massa de 4k g , e a engrenagem D tem uma massa de 5k g com um raio de giração ao centro de 64m m . A engrenagem maior B é fixa e não pode girar. Se o braço e a engrenagem
O veículo é utilizado para transportar suprimentos subindo e descendo a inclinação de 25 % . Cada par de rodas, um em A e outro em B , tem uma massa de 140k g com um raio de giração de 150m m . O tamb
Um sistema de engrenagens planetárias é apresentado, onde os dentes das engrenagens são omitidos da figura. Cada uma das três engrenagens planetárias idênticas A , B e C tem uma massa de 0,8k g , um r
A torre aérea mostrada é projetada para elevar um operário em uma direção vertical. Um mecanismo interno em B mantém o ângulo entre A B e B C igual a duas vezes o ângulo θ entre B C e o solo. Se a mas