Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas fundamentais - Ex. 16

Determine as componentes horizontal e vertical da reação no pino C .

Passo 1

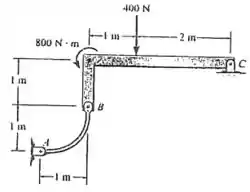
A fim de determinar as reações no pino C será necessário analisar o DCL do membro B C e fazer o equilíbrio de forças e aplicar o princípio dos momentos para ele. Isso servirá para que se descubra o valor das outras forças agindo sobre o membro em questão que terão influência sobre o valor das reações desejadas.

Passo 2

Logo, fazendo o DCL de B C tem-se:

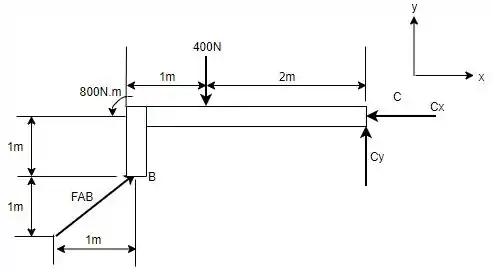
Passo 3

Agora, com o DCL é possível determinar o valor da força F A B para determinar as reações em C restantes.

Então, aplicando o princípio dos momentos, considerando que o momento seja positivo no sentido anti-horário, em relação ao ponto C :

∑ M C = 0 ⇒ 800 + 400 2 + F A B 1 2 1 - F A B 1 2 3 = 0

F A B 3 - 1 2 = 800 + 800

F A B = 1131,37   N

Passo 4

Enfim, com o valor de F A B é possível fazer o equilíbrio de forças para os eixos coordenados e determinar as reações.

Logo, para o eixo x :

∑ F x = 0 ⇒ - C x + F A B 1 2 = 0

C x = 1131,37 1 2

C x = 800   N

E para o eixo y , obtém-se:

∑ F y = 0 ⇒ C y + F A B 1 2 - 400 = 0

C y = 400 - 1131,37 1 2

C y = - 400   N

O sinal negativo indica que C y age no sentido oposto ao indicado no DCL. Logo, age para baixo.

Resposta

C x = 800   N

C y = 4 00   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força nos membros  E F ,  C F  e  B C da treliça. Indique se os membros estão sob tração ou  compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.
Determine a força nos membros EF, AF e DF da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por elos curtos em A, B, D e E.
. A treliça espacial é usada para suportar as forças nos nós B e D. Determine a força em cada membro e indique se os membros estão sob tração ou compressão.