Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 63
Atreliça espacial mostrada está presa aos suportes fixos em , e e está carregada pela força , que tem componentes e iguais mas não tem componente (vertical). Mostre que existe um número suficiente de elementos para garantir estabilidade interna e que seu posicionamento é adequado para esse objetivo. Em seguida determine as forças nos elementos , e .
Passo 1
Para uma treliça espacial estaticamente determinada como um todo, se temos nós e elementos, teremos equações de estabilidade (3 equações de força para cada nó) e incógnitas (uma para cada elemento e 6 para forças externas atuando na treliça). Então a treliça deve satisfazer a relação . Nesse caso, temos e , então temos
E a condição é satisfeita. Além disso, todos os nós pertencentes à treliça estão em tetraedros rígidos formados por 4 pontos, então cada um dos nós está fixado.
Passo 2
Todas as forças que queremos encontrar pertencem ao nó , então vamos resolver as condições de equilíbrio para esse nó. Mas temos 4 incógnitas nesse ponto e só 3 equações, então antes devemos encontrar a partir das equações do nó .
Achamos o ângulo através de sua tangente:
Pela soma das forças no eixo :
Agora em :
Passo 3
Agora podemos fazer as equações para o nó .
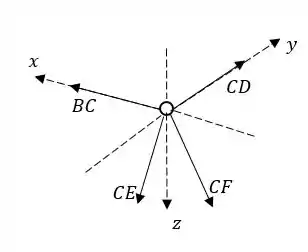
Vamos colocar e na forma vetorial e resolver para as 3 direções. Para temos:
Representamos pelo seu vetor unitário:
Em só temos como incógnita, então fazendo a soma das forças nessa direção:
Agora encontramos fazendo a soma para :
Finalmente fazemos para :