Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 37

A treliça Howe está sujeita ao carregamento mostrado. Determine as forças nos membros G H ,   B C   e   B G e indique se os membros estão sob tração ou compressão.

Passo 1

Oi, tudo bem? Vamos analisar esta questão.

Nesta questão vamos fazer algumas manipulações com as equações de equilíbrio. Portanto fique bem atento ao diagrama de corpo livre.

Passo 2

Vamos calcular o ângulo θ

tan ⁡ θ = 3 4

θ = 36.87 °

Vamos calcular o ângulo α

tan ⁡ α = 3 2

α = 56.3 °

Tomemos o momentos sobre A.

∑ M A = 0

E y 8 - 2 8 - 5 6 - 5 4 - 5 2 = 0

8 E y - 76 = 0

E y = 9.5   k N

Portanto, E y está a força de reação vertical no ponto E.

Passo 3

Vamos considerar o equilíbrio de força ao longo da direção y.

∑ F y = 0

A y + E y - 2 - 5 - 5 - 5 - 2 = 0

A y + 9.5 - 2 - 5 - 5 - 5 - 2 = 0

A y = 9.5   k N

Portanto, A y está a força de reação vertical no ponto A.

Vamos considerar o equilíbrio de forças ao longo da direção x

∑ F x = 0

A x = 0

Portanto, A x está a força de reação horizontal no ponto A.

Passo 4

Vamos cortar a treliça através dos membros G H ,   B G   e   B C , e vamos considerar a parte do lado esquerdo da treliça.

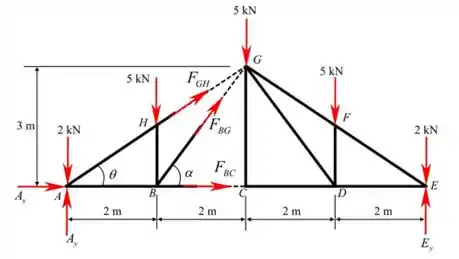
Passo 5

Vamos tomar o momento sobre G

∑ M G = 0

F B C 3 - A y 4 + 2 4 + 5 2 = 0

F B C 3 - 9.5 4 + 2 4 + 5 2 = 0

3 F B C - 20 = 0

F B C = 6.67   k N   ( T e n s ã o )

Portanto, a força no membro BC é 6.67   ( T )

Passo 6

Vamos tomar o momento sobre B

∑ M B = 0

2 2 - F G H cos ⁡ 36.87 ° × L B H - A y 2 = 0

Vamos encontrar o comprimento B H usando triângulos semelhantes A B H e A C G

L A C L C G = L A B L B H

4 3 = 2 L B H

L B H = 3 2

2 2 - F G H cos ⁡ 36.87 ° 3 2 - 9.5 2 = 0

- 15 - 1.2 F G H = 0

F G H = - 12.5   k N

F G H = 12.5   k N   C o m p r e s s ã o

Portanto, a força no membro G H é 12.5   k N   ( C )

Passo 7

Vamos considerar o equilíbrio de forças ao longo da direção x

∑ F x = 0

F G H cos ⁡ θ + F B G cos ⁡ α + F B C = 0

- 12.5 cos ⁡ 36.87 ° + F B G cos ⁡ 56.3 ° + 6.67 = 0

F B G = 6.01   k N   ( T e n s ã o   )

Portanto, a força no membro B G é 6.01   k N   ( T )

Resposta

Portanto, a força no membro BC é 6.67   ( T ) .

Portanto, a força no membro G H é 12.5   k N   ( C ) .

Portanto, a força no membro B G é 6.01   k N   ( T ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força nos membros B C , C H , G H e C G da treliça e indique se os membros estão sob tração ou compressão.
Determine a força nos membros B E , E F e C B e indique se os membros estão sob tração ou compressão.
Determine a força nos membros B F , B G e A B e indique se os membros estão sob tração ou compressão.
Determine a força nos membros B C , H C e H G . Indique se os membros estão sob tração ou compressão.
Determine a força nos membros E F ,E P e L K da treliça de ponte Baltimore e indique se os membros estão sob tração ou compressão. Além disso, indique todos os membros de força zero.