Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 44

Um trem de carga parte do repouso e move-se com aceleração constante de 0,15   m / s 2 . Após um tempo t ' , ele mantém uma velocidade escalar constante de maneira que quando t = 160 s ele percorreu 600 m. Determine o tempo t ' e trace o gráfico v - t para o movimento.

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade e deslocamento inicial:

v 0 = 0   m / s

s 0 = 0   m

No intervalo 0 ≤ t ' :

a = a 1 = 0,15   m / s 2

v = v 1

s = s 1

No intervalo t ' ≤ t :

a = a 2 = 0

v   é   c o n s t a n t e

v = v 2

s = s 2

No instante t = 160 s:

v 3 = v 2

s = s 3 = 600   m

Devemos determinar o tempo t ' e traçar o gráfico v - t para o movimento do trem.

Passo 2

Primeiramente, vamos analisar o intervalo 0 ≤ t ' .

A distância percorrida neste intervalo pode ser encontrada utilizando a seguinte equação:

s = s 0 + v 0 t + 1 2 a t 2

Logo,

s 1 = s 0 + v 0 t + 1 2 a 1 t 2

s 1 = 0 + 0 + 1 2 ( 0,15 ) t 2

s 1 = 0,075 t 2

Como queremos saber a distância percorrida até o instante t ' , podemos dizer que

s 1 = 0,075 t ' 2

Agora vamos achar a equação da velocidade para este intervalo. Sabemos que

v = v 0 + a t

Logo,

v 1 = v 0 + a 1 t

v 1 = 0 + ( 0,15 ) t

v 1 = 0,15 t

Passo 3

Em seguida, vamos analisar o intervalo t ' ≤ t .

Neste intervalo, a 2 = 0 pois a velocidade é constante. A velocidade será igual à v 2 = 0,15 t ' durante todo este intervalo.

Como a velocidade é constante, podemos utilizar a seguinte relação

v = ∆ s ∆ t

Onde, neste intervalo, v = v 2 , ∆ s = s 2 e ∆ t = ( 160 - t ' ) .

Logo, temos

v 2 = s 2 ( 160 - t ' )

s 2 = v 2 160 - t ' = 0,15 t ' ( 160 - t ' )

s 2 = 24 t ' - 0,15 t ' 2

Passo 4

Agora vamos analisar o instante t = 160 s.

Nesse instante, a distância total percorrida será

s t o t a l = s 1 + s 2 = s 3

Logo,

0,075 t ' 2 + 24 t ' - 0,15 t ' 2 = 600

0,075 t ' 2 - 24 t ' + 600 = 0

A equação de segundo grau acima possui duas raízes positivas:

r 1 = 27,335

r 2 = 292,665

Como a raíz r 2 é superior à 160, o valor de t ' será igual à raíz r 1 .

Portanto,

t ' = 27,34   s

Passo 5

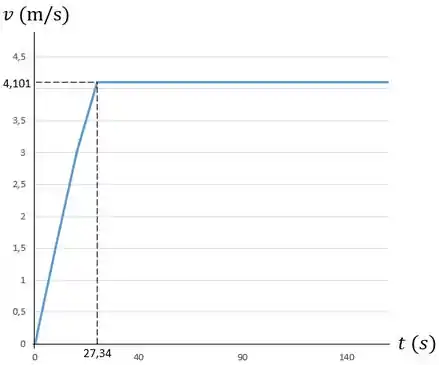
Vamos traçar o gráfico v - t .

Em t = 0 :

v = 0   m / s

No intervalo 0 ≤ t ' :

v 1 = 0,15 t

No intervalo t ' ≤ t :

v 2 = 0,15 t ' = 0,15 27,34 = 4,101   m / s

No instante t = 160 s:

v 3 = v 2 = 4,101   m / s

Plotanto esses pontos, teremos

Resposta

t ' = 27,34   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião pousa a 75m/s em uma pista reta e temm uma desaceleração descrita pelo gráfico. Determine a distância s’ percorrida antes que a sua velocidade escalar seja reduzida a 7,5 m/s. Trace o grafico
Um avião move-se ao longo de umna pista reta com uma aceleração descrita pelo gráfico. Se ele parte do repouso e precisa de uma velocidade de 90m/s para decolar, determine o comprimento de pista minim
Se as componentes x e y da velocidade de uma partocula são v x ( 32 t ) m/s e m/s, determine a equação da trajetória y = f ( x ) . x = 0 e y = 0 quanto t = 0
Uma partícula move-se ao longo de uma trajetória de uma linha reta y = 0,5 x . Se a componente da velocidade da partícula é v x = ( 2 t 2 ) m/s, onde t é dado em segundos, determine a intensidade da v
Uma partícula está se movendo ao longo de uma trajetória reta. Se a sua posição ao longo do eixo x é x = ( 8 t ) m , onde t é dado em segundos, determine sua velocidade escalar quanto t =2 s .