Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 28

Um trem de metrô com três vagões está percorrendo uma descida com de inclinação quando os freios individuais dos vagões são acionados simultaneamente. Cada vagão de pode gerar uma força de frenagem de vez a força normal exercida sobre ele pelos trilhos. Determine a desaceleração do trem e as forças e nos engates e para os casos em que

(a) todos os freios funcionam normalmente,

(b) os freios do vagão falham,

(c) os freios do vagão falham, e

(d) os freios do vagão falham.

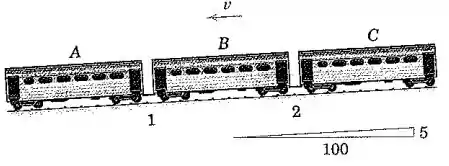
Passo 1

(a) Seja a força de frenagem que cada vagão pode gerar, a força peso de cada vagão, e a normal sobre cada vagão. Considerando a direção de inclinação como a direção , e a direção perpendicular como , podemos afirmar que existe equilíbrio em para cada vagão:

Agora aplicamos a Segunda Lei de Newton ao trem na direção , quando todos os freios funcionam normalmente:

Para uma inclinação de , isso significa que o ângulo satisfaz:

Então a aceleração do trem será:

Passo 2

Para calcular as forças e , podemos aplicar a Segunda Lei de Newton a cada vagão separadamente. Para o vagão , temos:

Aplicando agora a Segunda Lei de Newton ao vagão :

Passo 3

(b) No caso em que os freios do vagão falham, aplicamos a Segunda Lei de Newton ao trem na direção :

Aplicamos a Segunda Lei de Newton ao vagão separadamente, lembrando que seus freios falham:

Aplicando agora a Segunda Lei de Newton ao vagão :

Passo 4

(c) No caso em que os freios do vagão falham, a força resultante e a massa total do trem continuam as mesmas de quando os freios do vagão falham, ou seja, a equação da Segunda Lei de Newton aplicada ao trem na direção ficaria exatamente igual ao do item (b):

o que nos dá a mesma aceleração calculada anteriormente:

Aplicando a Segunda Lei de Newton ao vagão separadamente, obtemos :

É interessante notar aqui que o sinal deu negativo porque, ao contrário do que supusemos para o cálculo, a força empurra o vagão morro abaixo. Então, em módulo:

Aplicamos agora a Segunda Lei de Newton ao vagão , lembrando que seus freios falham:

Passo 5

(d) Novamente, quando os freios do vagão falham, a força resultante e a massa total do trem continuam as mesmas de quando os freios de qualquer um dos outros dois vagões falham, então a aceleração será a mesma:

Note que, quando os freios do vagão ou falham, a força resultante, a massa e a aceleração do vagão são as mesmas, e portanto, teremos a mesma força obtida no item anterior, quando os freios de falharam:

Aplicando agora a Segunda Lei de Newton ao vagão , cujos freios falharam:

Resposta

(a) ,

(b) , ,

(d) , ,

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo de uma linha reta com uma velocidade v = 20 - 0,05 s 2 m / s , onde s é dado em metros. Determine a aceleração da partícula em s = 15m .

Uma partícula move-se ao longo de uma linha reta com uma velocidade de v = 4 t - 3 t 2 m s , onde t é dado em segundos. Determine a posição da partícula quando t = 4s . s = 0 quando t = 0 .

Uma partícula se move ao longo de uma linha reta com uma aceleração de a = 10 - 0,2 s m / s 2 , onde s é medido em metros. Determine a velocidade da partícula quando s = 10m se v = 5m / s em s = 0 .

A aceleração de uma partícula se movendo ao longo de uma linha reta é a = k / v , onde k é uma constante. Se s = 0 , v = v 0 quando t = 0 , determine a velocidade da partícula como uma função do tempo

Um carro está se movendo a 15m / s , quando um semáforo, 50m à sua frente, acende a luz amarela. Determine a desaceleração constante exigida do carro e o tempo necessário para parar no semáforo.