Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 114
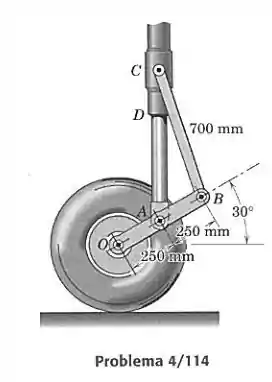
O trem de pouso do avião consiste no cilindro com pistão hidráulico e mola, e nas duas conexões articuladas e . Se a roda está se movendo ao longo da pista a velocidade constante e suportando uma carga constante e estável de 24 kN, calcule a força total suportada pelo pino em .
Passo 1
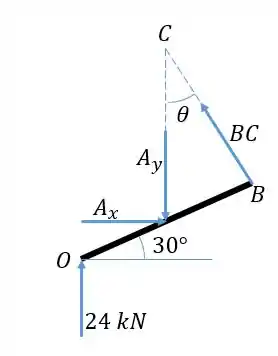
Primeiro vamos entender o que está acontecendo. A roda estar se movendo sob velocidade constante significa que está em equilíbrio, então a resultante das forças e dos momentos sob o corpo é zero. Se a roda suporta uma carga de 24 kN, então a força normal que o chão deve aplicar sobre a roda é de 24 kN, e pelo equilíbrio da roda o pino deve obrigatoriamente fazer uma força para baixo de 24 kN na roda. Devemos supor que não há forças horizontais sobre a roda. Então vamos representar a conexão em diagrama de corpo livre, pois nela temos as forças relevantes para o nosso cálculo. Perceba que a força em é para cima, pela lei da ação e reação entre a roda e o pino. Consideramos os pinos como se fossem parte da conexão :
Passo 2
Como e tem linha de força passando por , calculamos diretamente fazendo o momento ao redor de , mas precisamos da distância entre e . Vamos então calculá-la:
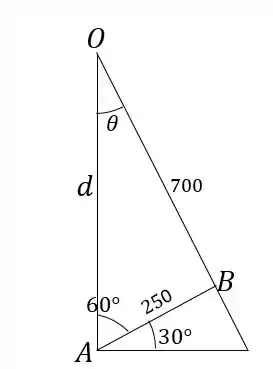
No triângulo , temos 2 pares de ângulo/lado opostos. Vamos então usar a lei dos senos para achar . Ela diz que para qualquer triângulo a razão entre o seno de um ângulo e o tamanho do lado oposto a esse ângulo é a mesma para os 3 vértices! Então:
Agora vamos usar a lei dos senos de novo pra encontrar . O outro ângulo, , tem o seguinte tamanho:
Então:
Passo 3
Então fazemos o momento em torno de :
Passo 4
Encontramos e fazendo as equações de força:
Passo 5
Agora que já temos as forças em , basta calcular o módulo: