Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 63
63- Duas forças e no espaço têm a mesma intensidade . Demonstre que o momento de em relação a linha de ação de é igual ao momento de em relação a linha de ação de .
Passo 1
Vamos desenhar duas forças em vetores quaisquer:
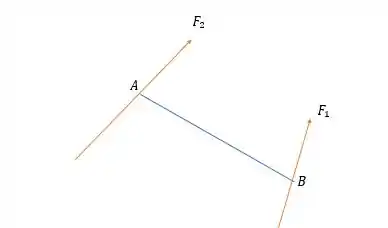
Vamos considerar que no vetor onde se encontra a força tem um ponto e a força tem um ponto . E o vetor da força e são iguais a:
Passo 2
O momento causado por no vetor onde encontra-se vale:
Pois é a distância relativa do ponto para . Agora o momento causado pela força no vetor onde encontra-se vale:
Pois é a distância relativa do ponto para e:
Pois é o sentido contrário de um para o outro.
O que é:
Pois e são vetores e e são escalares.
Passo 3
Porém e tem a mesma intensidade e que valem . Logo:
Agora aplicando
Temos:
Porém existe uma propriedade de determinante que nos diz que se o determinante de:
Se invertermos uma linha com a outra teremos:
O sinal do determinante troca. Logo:
Então o momento de em é igual ao momento de em , ou:
Resposta
Ei, a resposta está no passo a passo :)