Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 41
Determine as forças nos elementos , e .
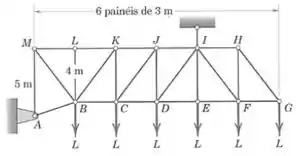
Passo 1
Já que temos uma força desconhecida agindo no ponto , vamos começar calculando o momento em relação a esse ponto. Lembre-se de que cada trecho da treliça mede , então:
Passo 2
Como nosso objetivo é calcular forças que envolvem os pontos , e , vamos escolher uma seção apropriada para aplicar o método das seções:
E então vamos aplicar a condição de equilíbrio para as forças na vertical:
Perceba que esse é simplesmente o cosseno do ângulo que a força forma com a perpendicular. O enunciado já deu o comprimento , e deduzimos o de aplicando o teorema de pitágoras.
E aproveitando essa mesma seção, vamos calcular o momento em relação ao ponto , pois nesse caso vamos eliminar as forças e :
E o sinal negativo indica que ela é, ao contrário do nosso desenho, uma força de compressão.
Passo 3
Fica faltando apenas a força . Nesse caso é mais útil olhar apenas para o equilíbrio do ponto :
E para eliminar as variáveis desconhecidas, vamos tomar o equilíbrio das forças na direção vertical:
E o sinal negativo indica que a força aponta no sentido contrário ao que desenhamos.
Resposta
As forças são (compressão), (compressão) e (tração).