Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 139
Substitua o sistema de forças e momentos binário que agem sobre o bloco retangular por um torsor. Especifique a intensidade da força e o momento de binário do torsor e a posição onde sua linha de ação intercepta o plano .
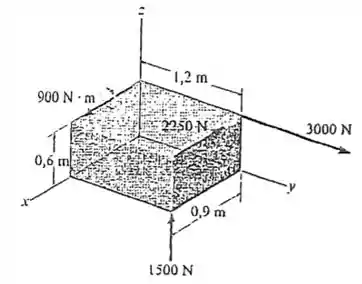
Passo 1
Falaa! O que a gente quer fazer ao achar um torsor para substituir esse sistema de forças é substituir essas forças por uma força resultante e um momento que tem o vetor na mesma direção da força, e aí podemos dizer que essa força e o momento são colineares.
Desejamos encontrar o módulo da força resultante e o momento binário do torsor além da posição onde sua linha de ação intercepta o plano .
Para encontrar as forças, a gente precisa apenas calcular o somatório das forças aplicadas. Isso é mais tranquilo de fazer usando forças na forma vetorial. Primeiramente podemos escrever as forças na forma de vetor cartesiano como sendo:
Percebe que a como as forças estão paralelas aos eixos coordenados, nós apenas colocamos a componente em cada força indicando a que eixo ela é paralela.
Tipo, a força é paralela ao eixo e está no seu sentido positivo, aí a gente só coloca o vetor unitário , para mostrar a direção dela. Já está no sentido negativo de , a gente coloca um sinal de menos e o vetor unitário .
A nossa força resultante vai ser a soma desses vetores
Logo a magnitude desse vetor será
Repara que aquele valor de é um momento aplicado. Aqui nas forças a gente não usa esse momento na análise. Vamos seguir!
Passo 2
Digamos que há um ponto sobre o plano , por onde passa a linha de ação do vetor do torsor . De coordenadas
E sabendo que é colinear a , nós podemos pensar que os dois vetores têm a mesma direção. Podemos achar uma expressão para o vetor de a partir do vetor unitário na direção de assim:
Percebe que aí estamos multiplicando o módulo do momento pelo vetor unitário na direção de . Substituindo os dados
Passo 3
Lembra que a gente disse que a linha de ação de passa por . Isso é o mesmo que dizer que é um momento em relação a .
E lembra quem é o nosso torsor? Ele deve ser a resultante dos momentos em relação a esse eixo que é colinear a .
Então, o que precisamos fazer é achar o somatório de momentos em torno desse eixo que passa por . E como a gente pode fazer isso? Calculando o somatório de momentos em relação a !
Como a gente já definiu a direção de , ao calcular o somatório de momentos em relação ao ponto , a gente garante que o resultado que vamos achar é o momento resultante no eixo que contem .
Os momentos são causados pelas forças , e . O resultante vai ser a soma desses momentos.
Vamos usar
Se a gente chamar de o ponto onde está aplicada, de o ponto de e o ponto de , para essas forças, o vetor vai ser o ponto de aplicação da força menos o ponto .
Nossas coordenadas são
Os vetores e são
Passo 4
Agora a gente lembra que o é o somatório de momentos em relação a e igual esse vetor a resultante de momentos que vamos calcular:
Somando os momentos de sobre o ponto e incluindo (não esquecendo de colocar a direção dele), vamos ter
Substituindo tudo o que achamos e já passando os produtos vetoriais para a carinha de determinante:
Isso vai resultar em
Passo 5
Fazendo a igualdade dos índices chegamos ao seguinte sistema
Resolvendo o sistema formado pelas equações acima vamos encontrar valores aproximados para dados pro
Pronto, finalmente está resolvido nosso exercício.