Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 114

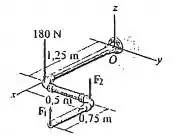
As três forças atuam no encanamento. Se F 1 = 50   N e F 2 = 80   N , substitua esse sistema de forças por uma força e momento de binário resultante agindo em O . Expresse o resultado na forma do vetor cartesiano.

Passo 1

O problema pede substituirmos o sistema de forças apresentado por uma força resultante e um momento de binário equivalente no ponto O . As forças que agem sobre a estrutura são

F 1 → = 50 k ^   N

F 2 → = - 80 k ^   N

F 3 → = - 180 k ^   N

A força resultante será

F R → = F 1 → + F 2 → + F 3 →

Assim,

F R → = 50 - 80 - 180 k ^   N

Logo,

F R → = - 210 k ^   N

Passo 2

Agora precisamos calcular os momentos de cada uma dessas forças com relação ao ponto O . Sabemos que o momento de uma força é dado por

M → = r → × F →

Assim, precisamos escrever o vetor posição de cada força relativo ao ponto O :

r 1 → = 2 i ^ + 0,5 j ^   m

r 2 → = 1,25 i ^ + 0,5 j ^   m

r 3 → = 1,25 i ^   m

Assim, vamos ter

M 1 → = 2 i ^ + 0,5 j ^ × 5 0 k ^   N ⋅ m = - 100 j ^ + 25 i ^   N ⋅ m

M 2 → = 1,25 i ^ + 0,5 j ^ × - 8 0 k ^   N ⋅ m = 100 j ^ - 4 0 i ^   N ⋅ m

M 3 → = 1,25 i ^ × - 180 k ^   N ⋅ m = 225 j ^   N ⋅ m

Somando todos os momentos:

M R → O = 25 - 40 i ^ + ( - 100 + 100 + 225 ) j ^   N ⋅ m

Portanto,

M R → O = - 15 i ^ + 225 j ^   N ⋅ m

Resposta

F R → = - 210 k ^   N

M R → O = - 15 i ^ + 225 j ^   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua a força de F = 80N que age sobre o encanamento por uma força e um momento de binário equivalentes no ponto A .
A correia passando pela polia está sujeita a duas forças F 1 e F 2 , cada uma tendo uma intensidade de 40N . F 1 atua na direção - k → . Substitua essas forças por uma força e um momento de binário eq
Determine o momento da força F = {50i - 40j + 20k} kN em relação ao eixo AB. Expresse o resultadocomo um vetor cartesiano.Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine o momento da força F em relação ao ponto O. Expresse o resultado como um vetor cartesiano.Fonte: Estática Mecânica para Engenharia – 14ª ed
A laje da construção está sujeita a quatro cargas paralelas das colunas. Determine a força resultante equivalente e especifique sua posição (x, y) sobre a laje. Considere F1 = 8 kN e F2 = 9 kN.