Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 143
Três forças atuam no ponto . Determine , e , se é conhecido que a componente da força resultante vale e que a componente vale .
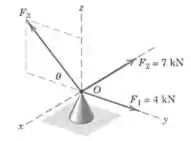
Passo 1
Primeiro vamos usar o fato de que a componente da força resultante . Como as forças e não tem nenhuma componente na direção de , a única contribuição nessa direção vem de :
Essa é a nossa primeira equação.
Passo 2
Agora vamos usar o fato de que a componente da força é :
E as contribuições nessa direção vêm das forças e :
E essa é a segunda equação.
Passo 3
Agora é só usar esse sistema para encontrar as variáveis:
Se dividirmos a primeira equação pela segunda:
Agora podemos substituir em qualquer uma das equações para encontrar :
Passo 4
E agora só falta calcular o módulo da força resultante . Para isso precisamos antes escrever sua forma vetorial:
Agora vamos calcular o módulo:
Resposta
, e .