Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 144
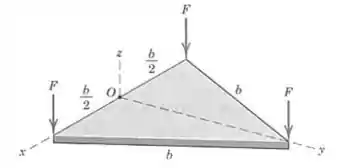
Três forças iguais são exercidas na placa equilátera conforme mostrado. Reduza o sistema de forças a um sistema força-binário equivalente no ponto . Mostre que é perpendicular a .
Passo 1
Para encontrar nosso sistema força-binário, primeiro precisamos calcular a força resultante :
Já que as três forças são todas iguais, e a forma vetorial de é:
E então:
Passo 2
Agora precisamos do momento dessas forças em relação ao ponto .
As duas forças que agem sobre o eixo tem momentos de mesmo módulo, mas favorecem a rotação em sentidos opostos, e por isso se anulam.
Falta calcular o momento da força que age sobre o eixo :
E então:
Esse é o momento do nosso sistema força-binário.
Passo 3
E usando a regra da mão direita, podemos ver que esse momento aponta na direção negativa do eixo :
(Obs: O produto vetorial que dá o momento é . Ao usar a regra da mão direira para encontrar a direção desse produto, você vai ver que seu polegar aponta no sentido negativo do eixo , por isso o .)
Agora podemos usar essa forma vetorial para provar que os vetores e são perpendiculares:
Substituindo com as expressões que encontramos:
Já que e são perpendiculares (por definição)
Resposta
O sistema força-binário é composto por e .