Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 41

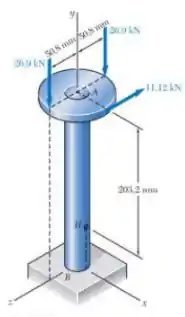
Três forças são aplicadas a uma placa com 101,6mm de diâmetro que está fixada a um eixo cheio AB de 45,7 mm de diâmetro. No ponto H, determine (a) as tensões e os planos principais e (b) a tensão de cisalhamento máxima.

Passo 1

E ai gurizada precisamos determinar (a) as tensões e os planos principais, vamos ao esboço :D

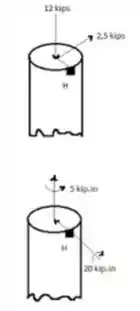
Na seção contando o ponto H, considere os dados: P = 12 k i p s   c o m p r e s s ã o   e   V = 2,5 k i p s

Calculando a torção temos:

T = 2 2,5 = 5 k i p     .     i n ,

M = 8 2,5 = 20 , k i p       .     i n .

Para determinar a área temos:

d = 1,8 i n .             c = 1 2 d = 0,9 i n .

A = π c 2 = 2,545 i n 2

E a inércia é dada por:

I = π 4 c 4 = 0,5153 i n 4

J = 2 I = 1,0306 i n 4

Passo 2

Para um semicírculo:

Q = 2 3 c 3 = 0,486 i n 3

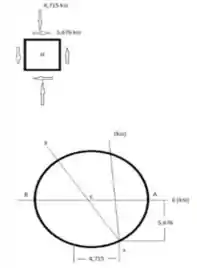
Ponto H no eixo neutro de dobra.

σ H = P A = - 12 2,545 = - 4,715 k s i

τ H = T c J + V Q I t = 5 0,9 1,0306 + 2,5 0,486 0,5153 1,8 = 5,676 k s i

Use círculo de Mohr:

σ a v e - 1 2 4,715 = - 2,3575 k s i

R = 4,715 2 2 + 5,676 2 = 6,1461 k s i

Passo 3

As tensões são dadas por:

  1.                                                                                                                         σ a = σ a v e + R                                                 σ a = 3,79 k s i    

    2.                                                                                               σ b = σ a v e - R                                             σ b = - 8,50 k s i        

    t a n 20 p = 2 5,676 4,715 = 2,408                       θ a = 33,7 0

    θ b = 123,7 0

  2. τ M A X = R

τ M A X = 6,15 k s i  

Resposta

  1. 123,7 0
  2. 6,15 k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O painel de sinalização uniforme pesa 7,5 kN e é suportado pelo tubo AB que tem raio interno de 68 mm e raio externo de 75 mm. Se a parte frontal do painel estiver sujeita a uma pressão uniforme do ve
A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto C e mostre os resultados em um elemento de volume diferencial nesse ponto.
A lança de guindaste é submetida a uma carga de 2,5 kN. Determine o estado de tensão nos pontos A e B. Mostre os resultados em um elemento de volume diferencial localizado em cada um desses pontos.
A haste maciça de 25 mm de diâmetro está sujeita às cargas mostradas na figura. Determine o estado de tensão no ponto B e mostre os resultados em um elemento diferencial localizado nesse ponto
A barra de distribuição de peso carregada simetricamente é usada para levantar o tanque de 10 kN (~1 tonelada). Determine o estado de tensão nos pontos A e B e indique os resultados em elementos de vo