Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 4
Três macacos , e , com massas de , e , respectivamente, estão subindo e descendo a corda suspensa a partir de . No instante representado, está descendo a corda com uma aceleração de , e está se puxando para cima com uma aceleração de . O macaco está subindo com uma velocidade constante de . Considere a corda e os macacos como um sistema completo e calcule a tração na corda em .
Passo 1
Galera, as únicas forças externas nesse caso são os pesos de cada macaco e a tração na corda em , pois as trações entre e ou entre e são forças internas ao sistema de macacos.
Então, representamos as forças externas na seguinte figura:
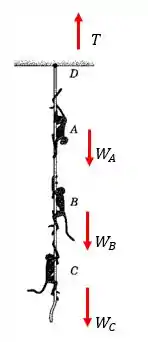
Passo 2
Agora, vamos aplicar a Segunda Lei de Newton ao sistema:
Resposta
Exercícios de Livros Relacionados
Um cilindro C de 8 kg repousa sobre uma plataforma A de 4 kg sustentada por uma corda que passa sobre as roldanas D e E e é presa a um bloco B de 4 kg. Sabendo que o sistema é liberado do repouso, det
O sistema mostrado na figura é liberado do repouso. Determine o tempo necessário para a velocidade de A atingir 1 m/s. Despreze o atrito e a massa das roldanas.
Um colar de 2 kg pode deslizar sobre uma barra vertical sem atrito e está sujeito a uma força P cuja intensidade varia como mostrado na figura. Sabendo que o colar está inicialmente em repouso, determ
Um caminhão-baú, com um cavalo mecânico de 2.000 kg um baú 8.000 kg, viaja em uma estrada nivelada a 90 km/h. Os freios da carreta do baú traseiro falham e o sistema antiderrapagem do cavalo-mecânico
Uma bola de golfe de 46 g é golpeada com um taco de golfe e o deixa a uma velocidade de 50 m/s. Consideramos que para 0 ≤ t ≤ t 0 , onde t 0 é a duração do impacto, a intensidade F da força exercida n