Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 31

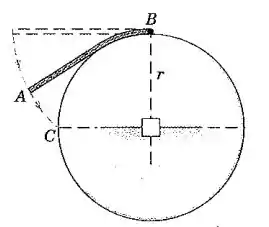
Uma corda flexível inextensível de massa ρ por unidade de comprimento e comprimento igual a 1 / 4 da circunferência do tambor fixo de raio r é liberada a partir do repouso na posição horizontal tracejada, com a extremidade B fixada no topo do tambor. Quando a corda finalmente atinge o repouso com a extremidade A em C , determine a perda de energia Δ Q do sistema. O que acontece com a energia perdida?

Passo 1

A perda de energia do sistema será calculada assim:

Δ Q = Δ T + Δ V g

Como a corda é liberada do repouso e depois atinge o repouso, temos Δ T = 0 . Desse modo:

Δ Q = Δ V g = V 1 - V 2

Na posição inicial (tracejada), o centro de massa da corda está a uma altura h 1 = r do centro do tambor, de modo que podemos escrever:

V 1 = m g h 1 = ρ l g r = ρ 1 4 2 π r g r = 1 2 ρ π r g r

V 1 = 1 2 π ρ g r 2

Passo 2

Agora, para calcular a energia V 2 , precisamos achar a altura h 2 do centro de massa quando a corda está na posição final. Para isso, podemos usar a fórmula:

h 2 = ∫ h   d m m

onde h é a altura de um ponto qualquer da corda e d m é a massa infinitesimal. Porém, pela geometria do problema, podemos escrever:

h = r cos ⁡ θ

onde θ é o ângulo partindo da vertical que passa pelo centro do círculo até o ponto h .

Ainda temos:

d m d l = ρ

d m = ρ   d l

Mas,

d l = r   d θ

Ou seja,

d m = ρ r   d θ

Passo 3

Assim sendo, obteremos:

h 2 = ∫ h   d m m = ∫ r cos ⁡ θ ρ r   d θ   1 2 ρ π r

h 2 = 2 π ∫ r cos ⁡ θ d θ

Olhando novamente para a figura, vemos que os limites de integração serão 0 e π / 2 :

h 2 = 2 π ∫ 0 π / 2 r cos ⁡ θ d θ = 2 π r   s e n π 2 - r   s e n   0

h 2 = 2 π r

Passo 4

Portanto,

V 2 = m g h 2 = 1 2 ρ π r g 2 π r

V 2 = ρ g r 2

E assim, obtemos a perda de energia:

Δ Q = V 1 - V 2 = 1 2 π ρ g r 2 - ρ g r 2

Δ Q = π 2 - 1 ρ g r 2

Δ Q = 0,571   ρ g r 2

Essa energia é perdida durante o impacto da corda com o tambor, na forma de calor.

Resposta

Δ Q = 0,571   ρ g r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pessoa que passa através da porta giratória exerce uma força horizontal de 90 N em um dos quatro painéis da porta. Se cada painel e modelado por uma placa retangular uniforme de 60 kg com 1,2 m de
O caminhão basculante transporta 5m 3 de terra com uma massa especifica de 1600k g / m 3 , e o mecanismo de elevação gira a caçamba em torno da articulação A a uma velocidade angular constante de 4gra
A empilhadeira com centro de massa em G 1 possui uma massa de 1600k g , incluindo o mastro vertical. O garfo e a carga têm uma massa combinada de 900k g , com centro de massa em G 2 . A guia rolante e
Uma barra esbelta de massa m 0 e comprimento l está soldada em seu ponto médio A na borda do disco circular macicço de massa m e de raio r . O centro do disco, que rola sem deslizar, tem uma velocidad
O bloco retangular uniforme com as dimensões fornecidas é deixado cair do repouso a partir da posição mostrada. A extremidade A atinge a borda em B e se prende a ela. Determine a velocidade angular ω