Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 68
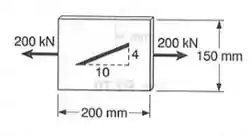
Uma linha de inclinação é desenhada sobre uma placa de latão-amarelo de de largura e de espessura. Usando a tabela apêndice B, para esse material, determinar a inclinação da linha quando a placa é submetida a uma carga axial centrada de , como indicada.
Passo 1
Para determinarmos o novo ângulo precisamos fazer o seguinte cálculo:
E os dados do enunciado são:
Assim o coeficiente de Poisson será dado por:
Sabemos que:
Sabemos que o comprimento do triangulo na direção x é de 10 e na direção y é de 4, com isso podemos fazer a seguinte conta:
Substituindo teremos que:
Resposta
Exercícios de Livros Relacionados
Um poste de concreto de 4ft é reforçado por quatro barras de aço, cada uma com um diâmetro de ¾ in. Sabendo que E S = 29x10 - 6p s ieE S = 3,6x10 6 p s i , determine a tensão normal no aço e no concre
O fio uniforme ABC, de comprimento 2l quando não esticado, é preso aos suportes mostrados na figura de lhe é aplicada uma força vertical P no ponto médio B. Designando por A a área da seção transversa
As hastes de aço BE e CD têm cada uma 16 mm diâmetro ( E = 200G P a ) ; as extremidades das hastes são de rosca única com passo de 2,5 mm. Sabendo que depois de perfeitamente ajustados, a rosca C é ap
A barra uniforme BC tem uma seção transversal de área A e é feita de um aço doce que pode ser considerado elastoplástico com um módulo de elasticidade E e uma tensão de escoamento σ E . Usando o siste
O elemento mostrado é constituído com um cilindro de aço com diâmetro de 25,4 mm e duas luvas com 38,1 mm de diâmetro externo ajustadas nas suas extremidades. Sabendo que E = 200G P a , determine (a)