Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 19

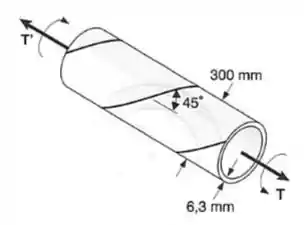
Um tubo de aço de diâmetro interno de 300   m m é fabricado a partir de uma placa de 6,4   m m de espessura, soldada ao longo de uma linha helicoidal, que forma um ângulo de 45° com um plano perpendicular ao eixo do tubo. Sabendo-se que a máxima tensão admissível de tração na solda é 80   M P a , determinar o maior torque que pode ser aplicado ao tubo.

Passo 1

O problema nos pede a tensão máxima admissível de tração, que para o caso de 45° será igual à tensão máxima de cisalhamento. Com isso vamos utilizar a nossa equação do torque:

τ = T ⋅ c J

Onde:

  • τ Representa a tensão de cisalhamento.
  • T A torção a qual a barra está submetida.
  • c A distância do centro ao ponto de aplicação.
  • J O momento de inércia polar.

Lembrando que o momento de inércia polar é calculado como:

J = π ⋅ c 4 2

Passo 2

Antes de calcularmos a tensão cisalhante, vamos calcular o momento de inércia polar. Lembrando que o momento de inércia polar J é calculado, para o caso de tubos vazados, como:

J = π ⋅ c e x t 4 2 - π ⋅ c i n t 4 2

Para o nosso tubo que possui:

  • raio externo igual a 150   m m .
  • raio interno igual a 150 - 6,3   m m = 143,7   m m :

J = π ⋅ [ 150 × 10 - 3 4 - 143,7 × 10 - 3 4 ] 2

J = π ⋅ [ 506.250.000 × 10 - 12 - 426.409.697 × 10 - 12 ] 2

J = π ⋅ ( 506.250.000 - 426.409.697 ) × 10 - 12 2

J = π ⋅ 79.840.303 × 10 - 12 2

J = 125.412.854 × 10 - 12 m 4

Passo 3

Agora vamos calcular o torque máximo:

τ = T ⋅ c J

Isolando o torque:

T = τ ⋅ J c

T = 80 × 10 6 ⋅ 125.412.854 × 10 - 12 150 × 10 - 3

T = 80 ⋅ 125.412.854 150 ⋅ 10 6 × 10 - 12 10 - 3

T = 66.886.855 ⋅ 10 - 3   N ⋅ m

T = 66.886 , 8 6   N ⋅ m

T = 66,89   k N ⋅ m

Resposta

T = 66,89   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao perfurar um poço a velocidade angular constante, a extremidade inferior do tubo de perfuração encontra uma resistência à torção T A . Além disso, o solo ao longo das laterais do tubo cria um torque
Os eixos de aço estão interligados por um filete de solda como mostra a figura. Determine a tensão de cisalhamento média na solda ao longo da seção a - a se o torque aplicado aos eixos for T = 60Nm .
O poste de madeira, o qual está enterrado no solo até a metade de seu comprimento, é submetido a um momento de torção de 50Nm que o faz girar a uma velocidade angular constante. Esse momento enfrenta
O eixo A B tem diâmetro de 30m m e é feito de um aço, com tensão admissível ao cisalhamento de 90M P a , enquanto que o eixo B C tem diâmetro de 50m m e é feito de uma liga de alumínio, com tensão adm
Dois eixos de aço são acoplados pelas engrenagens mostradas. Determinar a máxima tensão de cisalhamento em cada eixo, quando um torque T de 4k N ⋅ m é aplicado em D .