Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 10.Problemas - Ex. 56
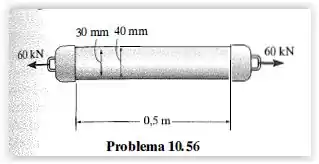
O tubo de aço está sujeito à carga axial de . Determine a mudança no volume do material após a aplicação da carga.
Passo 1
Vamos lá resolver esse problema?
O enunciado pede que determinemos a mudança no volume do material após a aplicação de uma carga axial .
Não temos tensão nem no eixo e nem no eixo , temos apenas a tensão provocada pela carga no eixo , que, como sabemos, corresponde a carga aplicada dividida pela área da seção transversal.
A deformação volumétrica pode ser expressa em termos da tensão aplicada. Assim, temos:
Através dessa equação, vamos encontrar a mudança de volume , solicitada na questão.
Passo 2
Sabemos que o volume do tubo é dado pela área da seção transversal vezes o comprimento do tubo, ou seja:
Colocando os dados na equação da deformação volumétrica, temos:
Substituindo as tensões e passando para o outro lado da equação:
Substituindo o volume por :
Divindo por , ou seja, cortando da equação:
Sunstituindo agora os valores numéricos: