Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 60
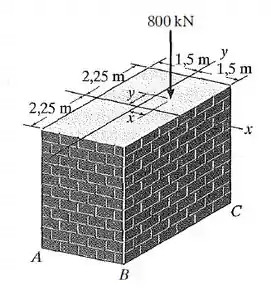
A pilastra de alvenaria está sujeita à carga de 800 kN. Se x = 0,25 m e y = 0,5 m, determine a tensão normal em cada canto A, B, C, D (não mostrado na figura) e trace a distribuição da tensão na seção transversal. Despreze o peso da pilastra.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que essa pilastra recebe uma carga conforme tá na figurinha.
Ele pede a tensão normal nos quatro cantos da seção transversal da pilastra. A tensão normal pode ser causada por esforço normal por momentos. Vamos começar achando esses esforços para nossa seção.
A gente vê que tem uma força na direção axial da nossa pilastra, normal a nossa seção. Então ela causa um esforço normal na viga:
Vemos também que essa força não está localizada na coordenada do centroide nem para nem para . Isso significa que a força causa momento em relação a esses dois eixos:
Aí agora o que a gente precisa é calcular as tensões normais causadas por esses esforços. Bora!
Passo 2
Vamos calcular algumas propriedades geométricas da nossa seção:
E as coordenadas dos nossos pontos:
Passo 3
Aí vamos montar uma equação para tensão que sirva para todos os nossos pontos de acordo com a coordenada deles. Isso vai agilizar nossas continhas.
Vemos que causa compressão, então ela entra na nossa fórmulinha como uma tensão negativa dada por
E o momento? Cara, o segredo aqui é ver pela figura que tipo de tensão os nossos momentos geram no primeiro quadrante, porque nele as coordenadas são positivas, não influenciam no sinal da tensão causada.
Esse é o . Ele causa compressão acima de , logo no primeiro quadrante ele causa compressão. A tensão causada por ele deve ter sinal negativo. E tem essa carinha:
Vamos olhar :
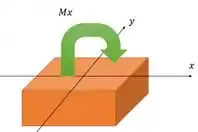
Ele também causa compressão no primeiro quadrante. Então fica com sinal negativo também.
Nossa fórmulinha geral fica:
Passo 4
Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo.