Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 112
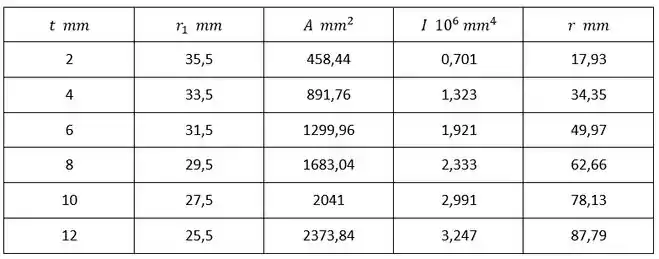
Um tubo de alumínio de de 75 mm de diâmetro externo e 2m de comprimento efetivo, deve suportar uma carga centrada de . Sabendo-se que os tubos disponíveis para o uso são feitos da liga e tem espessuras de parede a partir de 12 mm, em incrementos de 2 mm, determinar o tubo mais leve que pode ser usado.
Passo 1
E aí gurizada, vamos dar início aos nossos cálculos?!! Bora lá! O enunciado pede para determinar o tubo mais leve que pode ser usado
Passo 2
Agora podemos determinar a força P levando em conta os dados do enunciado e os que encontramos no anexo do livro :D
Resposta
Exercícios de Livros Relacionados
Uma coluna de aço de 6,6m de comprimento efetivo deve suportar uma carga excêntrica de 160 kN, em um ponto D localizado sobre o eixo x, como mostrado. Usando o método da interação, selecionar o perfil
Um membro de aço submetido à compressão, de 3,5m de comprimento efetivo, suporta uma carga excêntrica, como mostrada. Usando o método da interação, determinar a carga admissível P. Assumir E = 200 G p
Uma carga axial P de intensidade 670 kN é aplicada em um ponto sobre o eixo x, a uma distância e = 6,35mm do eixo geométrico do perfil laminado de aço W200 x 46,1 da coluna BC. Usando E = 200 GPa, det
Resolver o problema 159 usando o método da interação
Uma carga axial P é aplicada em um ponto sobre o eixo x, a uma distância e= 6,35 mm do eixo geométrico do perfil laminado de aço w 200x 46,1 Da coluna BC.