Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 47
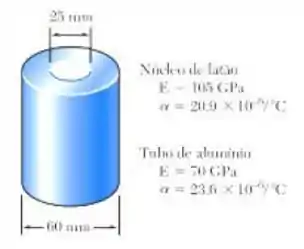
O tubo de alumínio é completamente unido ao núcleo de latão e a montagem tem as tensões aliviadas a uma temperatura de 15°C. Considerando apenas deformações axiais, determine a tensão ao alumínio quando a temperatura alcançar os 195°C.
Passo 1
Fala ai gurizada tudo belezinha?? O exercício pede para que a gente calcule a tensão no alumínio a 195°C, então vamos esboçar um desenho do tubo para melhor visualização....
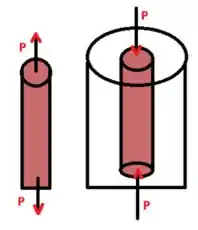
Extraindo os dados do enunciado temos:
Núcleo de latão:
Tubo de alumino:
Para determinarmos a expansão térmica temos que ver a variação dessa temperatura...
A deformação do latão é calculada como:
A deformação do alumínio é calculada como:
Expansão total da casca em relação ao núcleo:
Seja P a força tênsil no núcleo e a força compressiva na carcaça temos:
Antes vamos calcular a área:
Passo 2
A deformação do tubo de alumínio:
Antes vamos calcular a área:
A deformação total do elemento é dada por:
Substituindo pelas equações que determinamos no passo 1 temos....
Onde,
Então,
Agora sim gurizada podemos calcular a tensão 0//