Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 143

O tubo de alumínio tem 5   m m de espessura e dimensões de seção transversal externa mostradas na figura. Determine a máxima tensão de cisalhamento média no tubo. Se o tubo tiver comprimento de 5   m , determine o ângulo de torção. G a l = 28   G P a .

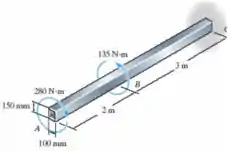
Passo 1

Os dados fornecidos pela questão: t = 5   m m ,   h = 150   m m ,   b = 100   m m ,   L = 5   m ,     G = 28   G P a .

A questão pede a tensão de cisalhamento média máxima no tubo e a deformação total no ponto C. Devemos ter atenção, pois esse é um tubo de paredes finas. A tensão de cisalhamento média máxima é encontrada pela equação 5.18. Já o calculo da deformação no ponto C é a soma das deformações ao longo do segmento AB e BC.

Passo 2

Começamos a questão desenhando um diagrama de corpo livre e calculando a reação de apoio em C.

∑ T = 0 ⇒ 250 - 135 - T c = 0

T c = 145   N m

Porém, se analisarmos as seções do tudo, percebemos que o maior torque ocorre ao longo da seção A B

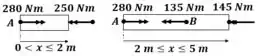
O maior torque que ocorre ao longo da estrutura é:

T A B = 280   N m

Passo 3

Esta é uma estrutura com paredes finas, então precisamos calcular a área interna média. Mas antes, definiremos a altura média e a base média:

h ' = h - t = 150 - 5 = 145   m m

b ' = b - t = 100 - 5 = 95   m m

A m = h ' ⋅ b ' = 145 ⋅ 95 = 13775   m m 2

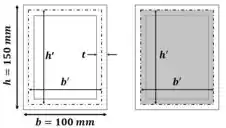
Passo 4

Aplicamos agora a equação 5.18

τ m e d = T 2 t ⋅ A m

τ m e d = 280 2 ⋅ 5 ⋅ 13775 ⋅ N ⋅ m m m ⋅ m m 2

τ m e d = 2,03   M P a

Passo 5

A deformação em uma extremidade é igual a soma dos segmentos:

ϕ c = ϕ A B + ϕ B C

Como estamos trabalhando com tubos de paredes finas, devemos utilizar a Equação 5.20

ϕ C = T A B L A B 4 ⋅ A m 2 ⋅ G ∮ d s t + T B C L B C 4 ⋅ A m 2 ⋅ G ∮ d s t

A espessura t é constante, e por isso pode sair da integral:

ϕ C = T A B L A B 4 ⋅ A m 2 ⋅ G ⋅ t ∮ d s + T B C L B C 4 ⋅ A m 2 ⋅ G ⋅ t ∮ d s

Colocando alguns fatores em evidência:

ϕ C = T A B L A B + T B C L B C 4 ⋅ A m 2 ⋅ G ⋅ t ∮ d s

A integral de linha de uma superfície fechada é o seu perímetro. Nesse caso, podemos substituir a integral pelo perímetro médio da seção:

ϕ C = T A B L A B + T B C L B C 4 ⋅ A m 2 ⋅ G ⋅ t 2 b ' + 2 h '

Simplificando:

ϕ C = T A B L A B + T B C L B C ⋅ b ' + h ' 2 ⋅ A m 2 ⋅ G ⋅ t

Aplicando os valores:

ϕ C = 280 ⋅ 2 + 145 ⋅ 3 ⋅ 95 + 145 2 ⋅ 13775 2 ⋅ 28 ⋅ 5 ⋅ N m ⋅ m ⋅ m m m m 4 ⋅ G P a ⋅ m m

ϕ C = 0,00449   r a d

ϕ C = 0,258 º

Resposta

τ m e d = 2,03   M P a

ϕ C = 0,258 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque de armazenamento contém propano líquido sob uma pressão de 1,5 MPa, a uma temperatura de 38 °C. Sabendo que o tanque tem um diâmetro externo de 320 mm e espessura de parede de 3 mm, determin
Um tubo de aço com diâmetro externo de 12 in. é fabricado a partir de uma chapa de espessura igual a 1/4 in. soldada ao longo de uma hélice que forma com o plano perpendicular ao eixo do tubo um ângul
Para o tanque de ar comprimido e o carregamento do Prob. 7.165, determine a tensão normal máxima e a tensão de cisalhamento máxima no plano no ponto b no topo do tanque.
O tanque de ar comprimido AB tem um diâmetro interno de 450 mm e espessura de parede uniforme de 6 mm. Sabendo que a pressão manométrica no tanque é de 1,2 MPa, determine a tensão normal máxima e a te
O tubo de latão AD é encaixado em uma jaqueta utilizada para aplicar uma pressão hidrostática de 3448 kPa à porção BC do tubo. Sabendo que a pressão interna do tubo é de 689,5 kPa, determine a máxima