Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 5
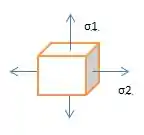
O tubo de extremidade aberta tem parede de espessura 2 mm e diâmetro interno de 40 mm. Calcule a pressão que o gelo exerceu na parede interna do tubo para provocar a ruptura mostrada na figura. A tensão máxima que o material pode suportar na temperatura de congelamento é σmáx = 360 MPa. Mostre como a tensão age sobre um pequeno elemento de material imediatamente antes de o tubo falhar.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que o nosso tubo tem paredes com 2mm de espessura e 20 mm de raio interno. Depois de falar isso tudo, ele nos pede a pressão necessária para romper a parede do nosso tubo. Viu?? Nem é tão difícil assim. Bora lá fazer?? Partiu??
Passo 2
Nas questões de vasos cilíndricos de paredes finas, temos duas tensões normais: σ1 (na direção circunferencial, ou seja, do aro) e σ2 (no sentido longitudinal, ou seja, axial). No nosso caso, sabemos que, como as extremidades são abertas, não teremos a tensão axial, apenas a circunferencial (a culpada por romper a parede interna).
Mas ele nos diz no enunciado que a tensão máxima é de 360 MPa, o que nos diz que, obrigatoriamente, a pressão interna foi alta o suficiente para fazer a tensão do aro chegar a esse valor. Então, temos que:
Passo 3
Sendo assim, achamos:
