Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 101
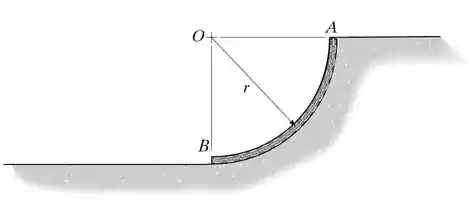
Um tubo AB forma um quarto de círculo de raio médio contém uma corrente lisa cuja massa por unidade de comprimento é . Se a corrente é solta do repouso da posição mostrada, determine a sua velocidade quando ela emerge completamente do tubo.
Passo 1
A localização do centro de gravidade da corrente para as posiçoes 1 e 2 são mostradas na figura abaixo.
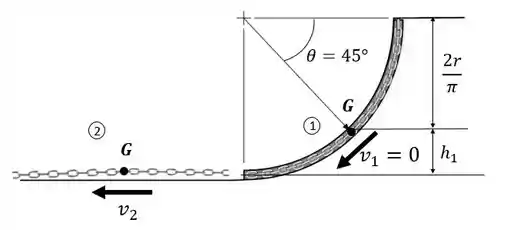
E a massa da corrente
E a altura para a posiçao 1 é
Passo 2
De acordo com a figura elaborada para resolver o problema as energias potenciais gravitacionais para as posições 1 e 2 são
Passo 3
Tento como referência a posição 2, a relação de conservação de energia
Resposta
A velocidade em que a corrente sair do tubo pode ser calculada por m/s
Exercícios de Livros Relacionados
As duas partículas de massas iguais estão ligadas por uma haste de massa desprezível. Se estas são liberadas a partir do repouso na posição mostrada e deslizam sobre a guia lisa no plano vertical, cal
Um cursor com uma massa de 0,25k g é liberado a partir do repouso em A e desliza para baixo e em torno do arame liso fixo. Determine a força N entre o arame e o cursor quando este passa o ponto B .
A mola tem um comprimento não esticado de 0,4m e uma rigidez de 200N / m . O cursor de 3k g e a mola conectada são liberados a partir do repouso em A e se deslocam no plano vertical. Calcule a velocid
A mola de constante k está sem deformação quando o cursor de massa m passa a posição B . Se o cursor é liberado a partir do repouso na posição A , determine sua velocidade quando este passa pelos pont
O cursor de 10k g desliza sobre a haste vertical lisa e tem uma velocidade v 1 = 2m / s na posição A onde cada mola está esticada de 0,1m . Calcule a velocidade v 2 do cursor quando este passa o ponto