Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 16
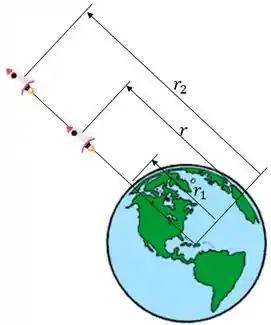
Um foguete de massa é lançado verticalmente da superfície da Terra, ou seja, em . Suponha que nenhuma massa é perdida à medida que ele se desloca para cima, determine o trabalho que ele precisa realizar contra a gravidade para chegar à distância . A força da gravidade é
Onde é a massa da Terra e é a distância entre o foguete e o centro da Terra.
Passo 1
O enunciado nos dá as seguintes informações:
Massa do foguete:
Nenhuma massa é perdida durante o trajeto.
A força da gravidade é igual a
onde e são conhecidas.
Devemos determinar o trabalho que o foguete precisa realizar para conseguir sair de e chegar à .
Passo 2
Sabemos que o trabalho realizado por uma força é dado por
Logo, na situação descrita pelo enunciado, teremos
Como e são constantes,
Resposta
Exercícios de Livros Relacionados
Uma haste esbelta de comprimento l e massa m está soldada na borda de um aro de raio l . Se o aro é liberado a partir do repouso na posição mostrada, determine a velocidade v do centro do aro, após te
A polia com raio de 400m m tem uma massa de 50k g e um raio de giração de 300m m . A polia e sua carga de 100k g estão suspensas pelo cabo e pela mola, que possui uma rigidez de 1,5k N / m . Se o sist
Um pequeno veículo experimental possui uma massa total m de 500k g , incluindo as rodas e o piloto. Cada uma das quatro rodas tem uma massa de 40k g e um raio de giração centroidal de 400m m . A resis
Cada uma das duas dobradiças em A e B , da tampa uniforme de massa m da caixa de brinquedos de uma criança, contém uma mola de torção que exerce um momento resistente M = K θ sobre a tampa enquanto es
O pequeno veículo é projetado para andar em alta velocidade sobre a neve. As lagartas em cada lado do veículo têm uma massa ρ por unidade de comprimento e são acionadas pelas rodas dianteiras. Determi