Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 18

O tubo de latão AB   E = 105   G P a tem área de seção transversal de 144 m m 2 e é ajustado com plugue em A. O tubo está conectado em B a uma placa rígida que, por sua vez, está conectada em C ao fundo de um cilindro de alumínio ( E = 72   G P a ) com seção transversal de 250 m m 2 . O cilindro é então suspenso por um suporte em D. Para fechar o cilindro, o plugue deve se mover para baixo em 1 mm. Determine a força P que deve ser aplicada ao cilindro.

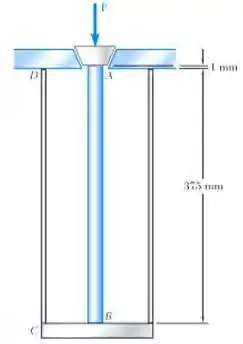
Passo 1

E ai gurizada tudo belezinha??? Para determinarmos a força P que deve ser aplicada ao cilindro, primeiramente vamos calcular o comprimento total

L A B = 375 + 1 = 376   m m = 0,376 m            

Dica, vamos passar a área para metros..

A A B = 140 m m 2 = 140   x   10 - 6 m 2

O alongamento é dado por... δ A B =   P L A B E A B A A B =   P   x   0,376 105   x   10 9     x   140   x   10 - 6 = 25,578   x   10 - 9 P

Passo 2

Agora vamos calcular o alongamento do cilindro de alumínio no trecho CD:

L C D = 0,375 m           A C D = 250   m m 2 = 250   x   10 - 6 m 2                 E C D = 72   x   10 - 9 P a

δ C D = P L C D E C D A C D =   P   x   0,375 72   x   10 9     x   250   x �� 10 - 6 = 20,833   x   10 - 9 P

A deflexão total é a soma das deformações em todo o elemento:

δ A =   δ A B + δ C D     o n d e       δ A = 0,001 m

Agora sim podemos encontrar P :D 0,001 = 25,578   x   10 - 9 + 20,833   10 - 9 P

P = 21,547   x   10 3

Resposta

P = 21,5   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determi
Um quadrado ABCD de 50mm de lado é riscado sobre a superfície de uma placa fina, quando a placa está sem carga. Depois da placa ser carregada, observou=se que os comprimentos dos lados AB e AD foram a
No P r o b . 6.100 , determinar o máximo valor admissível para h , sabendo-se que a tubulação é feita de um aço com uma tensão ultima a tração de 450M p a e que um coeficiente de segurança de 4,50 é d
Para o reservatório de ar comprimido do P r o b . 6.104 , determinar a maior pressão admissível, sabendo-se que a tensão normal admissível perpendicular a solda é de 165M p a e a tensão admissível de
A porção cilíndrica do reservatório de ar comprimido mostrado é fabricada de uma chapa de 5 m m de espessura soldada ao longo de uma hélice, formando um ângulo de 25 ° com o plano transversal ao eixo