Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 36
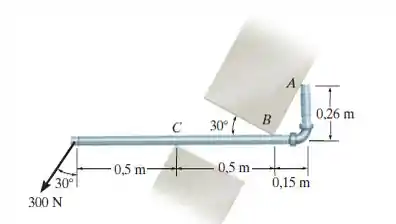
O tubo liso é encostado na abertura, nos pontos de contato e . Determine as reações nesses pontos, necessárias para suportar a força de . Para o cálculo, desconsidere a espessura do tubo.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar as reações nas superfícies lisas , e , as quais serão normais as respectivas superfícies.
Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Então, o nosso diagrama de equilíbrio será:
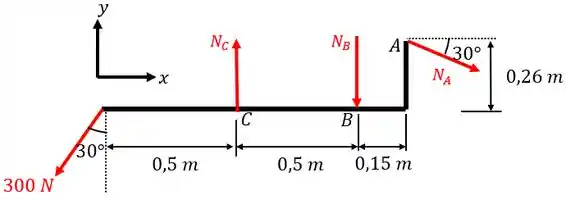
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar determinando a reação . Para isto, vamos fazer o somatório de forças na direção , pois, das nossas incógnitas, apenas a normal possui componente nesta direção.
Desta forma, temos:
E assim descobrimos a nossa primeira incógnita!
Passo 3
Agora, vamos determinar as outras duas.
Começaremos pelo cálculo de . Para isto, temos que calcular o somatório do momento em relação ao ponto , pois assim eliminamos a reação deste ponto na nossa equação.
Desta forma, temos:
E assim descobrimos a nossa segunda incógnita! Para finalizarmos, vamos fazer o somatório de momentos em torno do ponto . Desta forma, temos:
E assim finalizamos a questão!