Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 102
O dispositivo mostrado é útil para suspender e posicionar painéis antes de prendê-los aos tirantes na parede. Estime o módulo da força necessária para erguer o painel de . Explicite quaisquer suposições.
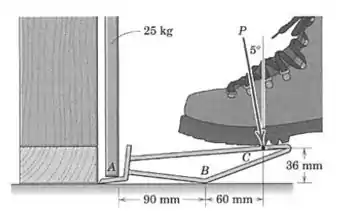
Passo 1
Vamos supôr que o painel é levantado na direção vertical, perfeitamente perpendicular ao chão. Nesse caso podemos desenhar as forças da seguinte forma:
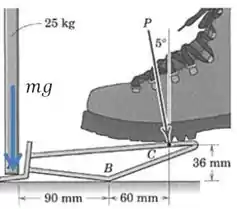
Ok, agora vamos procurar equações de equilíbrio para resolver o sistema, já que quando o painel está prestes a ser erguido, o sistema está em equilíbrio.
Passo 2
Existe também uma força de reação noral em , mas como não conhecemos essa variável, vamos escolher uma equação de forma que ela desapareça.
Em outra palavras, vamos usar a condição de equilíbrio dos momentos em relação ao ponto :
Nesse caso temos a componente da força na direção perpendicular ao painel (a do ponto ), e a componente na direção paralela ao painel (a do ponto ). Além disso temos o peso do painel a do ponto .
Resposta
O módulo necessário para a força é .