Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 15
O motor de Mg está suspenso por uma viga transversal de massa desprezível e é içado por um guindaste que exerce uma força de kN no cabo de içamento. Determine a distância pela qual o motor é içado em s, partindo do repolso.
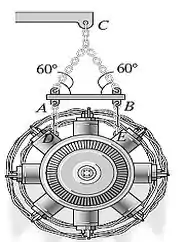
Passo 1
O primeiro passo é calcular a aceleração transversal do motor através da equação do movimento e, como se trata de uma aceleração constante, podemos determinar a distância pela qual o motor é içado em s, atraves da equação da cinemática para aceleração constante. Da equação de corpo livre, temos:
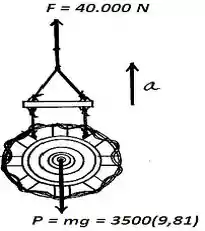
Passo 2
Agora que calculamos a aceleração do içamento, podemos determina a distância pela qual o motor é içado em s, atraves da cinemática para aceleração constante, assim:
Como o motor parte do repolso, sua velocidade inicial e deslocamento inicial será zero, então:
Passo 3
Substituindo o valor da aceleração do motor e o tempo , chegaremos ao seguinte valor da distância pela qual o motor é içado
m
Resposta
A distância pela qual o motor é içado em s é igual a m