Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 28

Os blocos A e B têm massa de m A e m B , sendo m A > m B . Se é dada uma aceleração de a 0 para a polia C, determine a aceleração dos blocos. Despreze a massa da polia.

Passo 1

Temos um problema que envolve polia! Começaremos analisando a cinética do problema, esboçando o diagrama de corpo livre de cada um dos blocos, para despois partirmos para a parte de cinemática, relacionando as acelerações dos blocos com a da polia para que possamos resolver o nosso problema! Temos que tomar muito cuidado nesta última etapa!!!

Passo 2

Começaremos esboçando o diagrama de corpo livre dos nossos blocos. Ambos os blocos possuem um diagrama bastante semelhante, mudando apenas o valor da componente do peso. Sendo assim, temos:

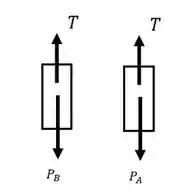
Sendo assim, ao fazermos o somatório ao longo do eixo y , obteremos:

T - m A g = m A a A

T - m B g = m B a B

Ao igualarmos as equações acimas, eliminando então a tração T , temos:

m A - m B g = m B a B - m A a A

Chegamos agora em um impasse. Temos uma única equação que envolve a aceleração de ambos os blocos! Precisamos de novas equações para que consigamos duas equações, sendo uma delas em função de a A e outra a B apenas!!! Para isto, partiremos para analisar a cinemática do problema!

Passo 3

Na nossa análise da cinemática, trabalharemos com acelerações relativas. A aceleração relativa do bloco A em relação a polia, e a do bloco B em relação a polia, são iguais entre si, tanto em módulo quanto em sentido! Isto decorre do fato delas estarem ligadas por um cabo. Portanto, temos:

a r e l = a A / P = a B / P

Agora, ao esboçarmos as equações da aceleração relativa dos blocos em relação a polia, obteremos:

a A = a P + a A / P = a 0 + a r e l

a B = a P + a B / P = a 0 + a r e l

Portanto, ao eliminarmos o termo a r e l , obtemos:

a A + a B = 2 a 0

Finalmente, obtemos uma outra equação que relaciona as duas acelerações. Ao resolvermos este sisteminha de equações, saberemos que as acelerações dos blocos A e B serão dadas por:

a A = 2 m B a 0 - m A - m B g m A + m B

a A = 2 m A a 0 + m A - m B g m A + m B

Resposta

a A = 2 m B a 0 - m A - m B g m A + m B

a A = 2 m A a 0 + m A - m B g m A + m B

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um foguete de dois estágios é lançado verticalmente para cima e está acima da atmosfera quando a combustão do primeiro estágio se extingue e o segundo estágio se separa e entra em ignição. O segundo e
O foguete apresentado é projetado para testar o funcionamento de um novo sistema de orientação. Quando ele atinge uma determinada altitude fora da influência efetiva da atmosfera terrestre, sua massa
Um jato de água doce sob pressão escoa a partir do bocal fixo com 20m m de diâmetro a uma velocidade v = 40m / s e é desviado nos dois escoamentos iguais. Despreze qualquer perda de energia nos escoam
Uma corda ideal ou uma corrente do tipo usado em bicicleta com comprimento L e massa ρ por unidade de comprimento está em repouso sobre uma superfície horizontal lisa quando a extremidade A volta sobr
As três esferas idênticas, cada uma de massa m , estão apoiadas no plano vertical sobre o plano inclinado de 30 ° . As esferas estão soldadas às duas hastes de conexão de massa desprezível. A haste su