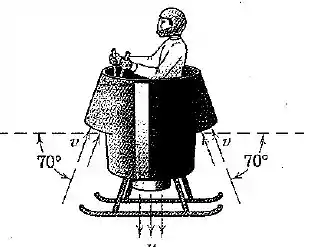
A viabilidade de uma aeronave (na sigla em inglês para decolagem e aterrisagem vertical) para apenas um passageito está sendo analisada. O projeto preliminar utiliza um pequeno motor com uma alta razão potência/peso para acionamento de uma bomba de ar que aspira o ar através dos dutos a com uma velocidade de entrada a uma pressão estática manométrica de através das áreas de admissão que totalizam . O ar é descarregado verticalmente para baixo com uma velociade . Para um passageiro de , calcule a massa líquida máxima do equipamento para o qual esse pode decolar e pairar. (Veja a tabela para a massa específica do ar.)

Vamos olhar para a equação para a força resultante que gera o escoamento do ar:

Podemos calcular a taxa de escoamento de massa do sistema usando os dados do enunciado:

E agora vamos calcular a variação de velocidade nessa direção:

E projetando essa velocidade na direção vertical :

E a velocidade final (que já é paralela a direção ) é:

Que aparece com sinal negativo porque aponta para baixo. Agora nossa equação da força resultante fica:

O próximo passo é projetar as nossas forças na direção também:

E então:

Agora é só resolver para encontra a massa: