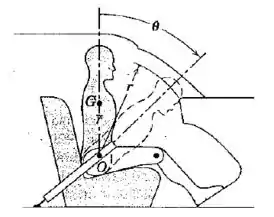
Em um estudo da lesão na cabeça contra o painel de instrumentos de um carro durante paradas bruscas ou em colisões onde cintos de segurança abdominais, sem alça no ombro, ou airbags são utilizados, o modelo humano segmentado mostrado na figura é analisado. Assume-se que articulação do quadril permanece fixa em relação ao carro, e o tronco acima do quadril é tratado como um corpo rígido de massa livremente articulado em . O centro de massa do tronco está em com a posição inicial de adotada como vertical. O raio de giração do tronco em relação a é . Se o carro é forçado a uma parada súbita com uma desaceleração constante , determine a velocidade em relação ao carro com a qual a cabeça do modelo atinge o painel de instrumentos. Substitua os valores , , , , e e calcule .

Vamos começar calculando o momento de inércia do tronco em relação ao centro de massa. Para isso vamos usar o teorema dos eixos paralelos:

E agora vamos montar uma equação de momentos em relação ao ponto :

E única força que produz momento em relação ao ponto é uma componente do peso, agindo sobre o centro de massa, a uma distância de :

E para esse último termo da equação de momentos, só precisamos considerar a aceleração tangencial associada à rotação em torno de , e a aceleração associada à desaceleração do carro. Ambas agem no centro de massa do tronco, a uma distância do ponto .

A aceleração centrípeta que age sobre o tronco não produz momento, pois sua linha de ação passa pelo ponto :

Agora vamos substituir tudo isso na equação principal:

E então podemos isolar a aceleração angular:

Agora podemos substiuir essa função na nossa integral do primeiro passo:

Vamos resolver essa integral separadamente:

Então:

Substituindo os valores numéricos:

E como a cabeça está a uma distância do ponto , a sua velocidade linear no instante em que colide contra o painel é: