O homem empurra a caixa de kg com uma força . A força é sempre direcionada para baixo a da horizontal, como mostrado, e sua intensidade é aumentada até a caixa começar a deslizar. Determine a aceleração inicial da caixa se o coeficiente de atrito inicial é e o coeficiente de atrito cinético é .
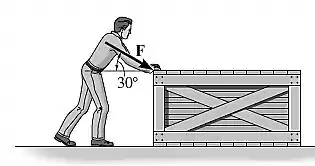
Passo 1
O primeiro passo é obter a força necessária para vencer a força de atrito estático entre a caixa e o plano. Esta força pode ser determinada através das equações de equilíbrio do sistema, então:
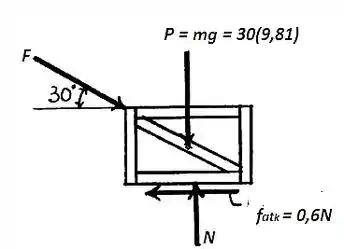
Resolvendo o sistema de equações, chegaremos aos seguintes valores para a força e a normal :
N
A força obtida é a força necessária para tirar a caixa do seu estado de repolso.
Passo 2
O próximo passo é determinar a aceleração inicial da caixa, através da equação do movimento. Do diagrama de corpo livre, temos:
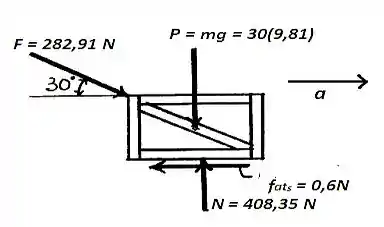
Passo 3
Isolando a celeração na equação acima, chegaremos ao seguinte valor:
Resposta
A aceleração inicial da caixa é igual a