Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 14

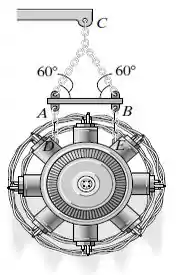
O motor de 3,5 Mg está suspenso por uma viga transversal A B de massa desprezível e é içado por um guindaste que dá a ele uma aceleração de 4 m / s 2   quando ele tem uma velocidade de 2 m / s . Determine a força nas correntes C A e C B durante o içamento.

Passo 1

Para determinarmos a força nas correntes C A e C B durante o içamento, preciamos inicialmente obter a força F desenvolvida no ponto C durante o processo, para isso, precisamos determinar a equação do movimento do sistema. Do diagrama de corpo livre, temos:

∑ F y = m a y

F - P = m a y

F - m g = m a y

F = g + a y m

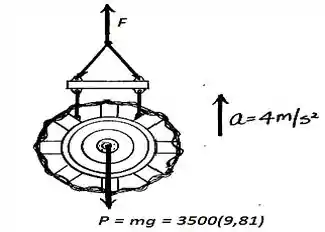
F = 9,81 + 4 3500 = 48,335   kN

Passo 2

Determinada a força de reação no ponto C , podemos obter a força nas correntes C A e C B através da equação de equilí brio do sistema, assim:

∑ F y = 0

F - 2 T cos ⁡ 30 = 0

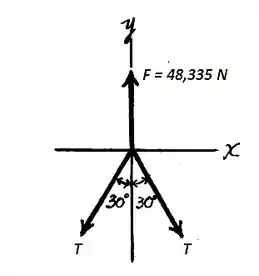
Isolando T na equação acima, temos:

T = F 2 cos ⁡ 30 0

Passo 3

Substituindo o valor da força F na equação acima, teremos o seguinte valor para a força T :

T = 48,335 2 cos ⁡ 30 0 = 27,9   k N

Resposta

A força nas correntes C A e C B durante o içamento é igual a 27 , 9   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carrinho transporta uma pilha de uma corrente de elos com massa ρ por unidade de comprimento. A corrente passa livremente através do orifício no carrinho e é conduzida ao repouso, elo por elo, pela
Uma corrente de elos de comprimento L = 8m com uma massa de 48k g repousa sobre uma superfície horizontal lisa quando a extremidade A volta sobre si mesma puxada por uma força P aplicada à extremidade
A corrente de elos de comprimento L e massa ρ por unidade de comprimento é liberada a partir de repouso mostrada, onde o elo mais baixo está quase tocando a plataforma e a seção horizontal é apoiada s
Na figura é apresentado um sistema utiliado para deter o movimento de um avião que pousa em um campo de comprimento restrito. O avião de massa m se deslocando livremente com uma velocidade v 0 se pren
Substitua a corrente do problema 4 / 88 por uma corda flexível ou uma corrente de bibicleta de massa ρ por unidade de comprimento e comprimento total L . A extremidade livre é liberada a partir do rep