Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 128
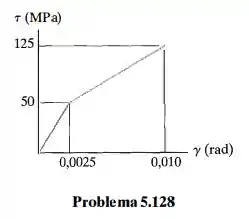
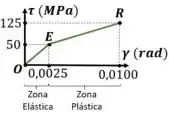
Um diagrama tensão-deformação por cisalhamento para um eixo maciço de 50 mm de diâmetro pode ser aproximado como mostra a figura. Determine o torque exigido para provocar uma tensão de cisalhamento máxima de 125 MPa no eixo. Se o eixo tiver 3 m de comprimento, qual será o ângulo de torção correspondente?
Passo 1
Dados da questão: Nesse material, tanto a zona elástica quanto a plástica possuem comportamento linear.
A questão afirma que a tensão na superfície do eixo é , o que implica que sua deformação é
O que a questão pede:
- O valor do torque aplicado
- O ângulo de torção plástico
Como o comportamento deste material é diferente do normal, vamos utilizar a equação 5.23 para determinar o torque.
Para aplicar a integração, precisaremos definir uma ou mais equações que representem o comportamento da tensão em função do raio.
Para relacionar a deformação com o raio, vamos considerar que a deformação é constante ao longo da seção transversal.
Para determinar o ângulo de torção basta aplicar a equação 5.25 para o valor de deformação máxima.
Passo 2
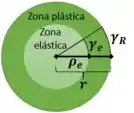
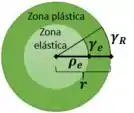
Primeiro, precisamos saber qual região o tamanho da zona elástica e da zona plástica. Faremos isso definindo o tamanho do raio elástico .
Por definição, no raio elástico a deformação é igual a deformação de escoamento. Podemos aplicar proporção para determinar o raio
Passo 3
Uma vez que consideramos que a deformação é linear ao longo da seção transversal, podemos garantir que a razão entre a deformação e o raio é contante:
A expressão pode ser manipulada como:
Passo 4
Vamos determinar uma equação que represente o segmento OE
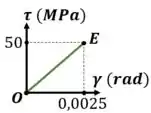
Por proporção, temos:
Isolando a tensão:
Substituíndo , como definido no passo anterior
Chegamos numa expressão que relaciona a tensão com o raio.
Substituíndo os valores:
Chegamos na equação:
Onde o raio é dado em metros, e a tensão é dada em . Vamos manter essas unidades de medida para evitar trabalhar com números muito grandes ou com potências de dez
Note que essa função é válida apenas elástico:
Passo 5
Vamos determinar uma equação que represente o segmento ER
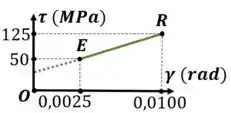
Por proporção, temos:
Isolando a tensão:
Substituíndo , como definido no Passo 2
Colocando em evidência chegamos numa expressão que relaciona a tensão com o raio:
Substituíndo os valores:
Chegamos na equação:
Onde o raio é dado em metros, e a tensão é dada em . Vamos manter essas unidades de medida para evitar trabalhar com números muito grandes ou com potências de dez
Note que essa função é válida apenas no intervalo plástico:
Passo 6
Em posse das funções que representam a tensão, podemos aplicar a Equação 5.23 para determinar a tensão:
Subtituíndo as funções de acordo com os respectivos limites
Vamos manipular a equação para simplificar ao máximo as integrais:
Aplicando as integrações:
Substituíndo os valores:
Obtemos um valor em mega newtons vezes metro, pois as tensões utilizadas nos cálculos anteriores estavam em mega pascal.
Passo 7
Aplicando a Equação 5.25 encontramos o ângulo de torção plástica