Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 93
O estado de tensões mostrado irá ocorrer em um componente de alumínio fundido. Sabendo-se que para a liga de alumínio usada = 60MPa
e = 120MPa, e usando o critério de Mohr, determinar a tensão de cisalhamento , para que a ruptura possa acontecer.
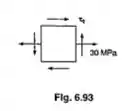
Passo 1
Nada como uma questãozinha de critério de Mohr para alegrar nosso dia né? Bora fazer junto?
O elemento nos foi dado com as seguintes tensões.
Pro critério de Mohr, precisamos achar as tensões principais. Então:
Passo 2
Agora vamos aplicar o critério de Mohr, que diz que pro material falhar deve ser atingido o valor abaixo:
Rearrumando:
Dividindo toda essa galera por 60 temos:
Passo 3
Show de bola, agora é só a gente lembrar que:
Rearrumando:
Substituindo r= 45.
Resposta
Exercícios de Livros Relacionados
Para a treliça de aço ( E = 200G P a ) e os carregamentos mostrados, determine as deformações dos componentes BD e DE, sabendo que suas áreas de seção transversal são, respectivamente, 1290 m m 2 e 19
A barra de conexão BD é feita de latão ( E = 105G P a ) e tem área de seção transversal de 240 m m 2 . A barra de conexão CE é feita de alumínio ( E = 72G P a ) e tem área de seção transversal de 300
O volume de um corpo de prova em tração é essencialmente constante enquanto ocorre a deformação plástica. Se o diâmetro inicial do corpo de prova for d 1 , mostre que, quando o diâmetro for d, a defor
Designando por ϵ a ‘’deformação especifica de engenharia’’ em um corpo de prova em tração, mostre que a deformação especifica verdadeira é ϵ p = l n ( 1 + ϵ ) .
Um cabo homogêneo de comprimento L e seção transversal uniforme é suspenso por uma das extremidades. (a) designado por p a densidade (massa por unidade de volume) do cabo e por E seu modulo de elastic