Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 119
Usando duas cordas e uma rampa de roletes, dois operários descarregam de um caminhão um contrapeso de ferro fundido de 890 N. Sabendo que, no instante mostrado, o contrapeso é mantido parado e que as posições dos pontos A, B e C são, respectivamente, A(0; -0,5 m; 1 m), B(-1 m; 1,3 m; 0) e C(1,1 m; 1 m; 0) e admitindo que não há atrito entre o contrapeso e a rampa, determine a tração em cada corda. (Dica: como não há atrito, a força exercida pela rampa sobre o contrapeso deve ser perpendicular à rampa).
Passo 1
Podemos escrever o somatório de forças no ponto A com o auxílio do diagrama a seguir como:
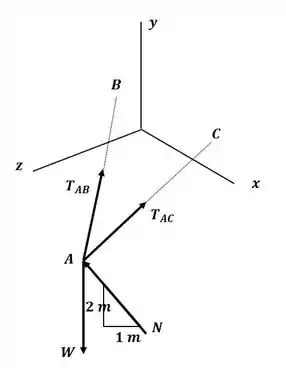
Agora precisamos escrever os vetores tensão e o vetor normal em termos de suas coordenadas, para isso, precisamos primeiro escrever o vetor que liga esses pontos, então:
Agora, calculando o módulo desses vetores:
Agora podemos escrever os vetores tensão e normal como:
Passo 2
Agora substituindo os valores das tensões na equação de equilíbrio de forças do passo 1, temos:
Agora vamos separar as componentes e :
Agora, substituindo o valor de W dado no enunciado, as equações se tornam:
Passo 3
Agora, isolando da terceira equação:
E, susbtituindo esse valor nas equações 1 e 2:
Substituindo esse valor na equação anterior:
Substituindo esse valor na equação para :
Agora, substituindo o valor de na primeira equação do passo 2: