Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 85
O letreiro tem massa de com centro de massa em . Determine as componentes , , da reação na junta esférica e a tração nos fios e .
Passo 1
Oie, tudo bem? Vamos analisar esta questão.
Nesta questão vamos fazer algumas manipulações com as equações de equilíbrio. Portanto fique bem atento ao diagrama de corpo livre.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio. Temos que:
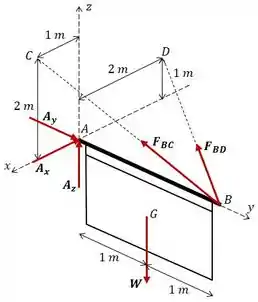
Onde o peso do letreiro é dado por:
Passo 2
Vamos começar então determinando vetorialmente as tensões nos fios e :
Além disso, a reação em é dada por:
Passo 3
Show de bola! Temos então pela condição de equilíbrio do corpo:
Substituindo os valores das forças nessa equação e separando nas coordenadas , e , temos:
Passo 4
Ou seja, até aqui temos 3 equações para 5 incógnitas. Para completar o nosso sistema de equações e determinar as reações em e as tensões nos fios, vamos considerar o somatório de momentos em torno do ponto :
Novamente, substituindo os valores das forças e dos vetores posição nessa equação e separando nas coordenadas , e . Para a componente , temos:
Já para a componente .
Substituindo essa relação de na equação anterior, temos:
Passo 5
Finalmente, substituindo esses valores nas equações do Passo 3 e resolvendo o sistema, temos que: