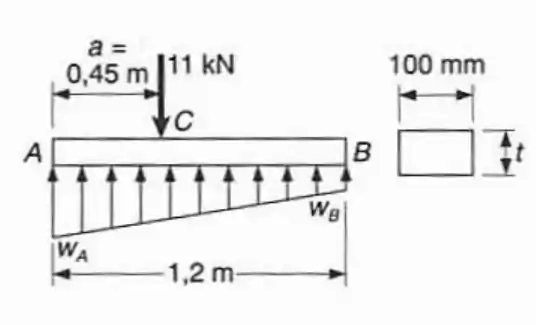
A barra de de largura suporta uma carga de e repousa sobre uma fundação, que exerce um carregamento linearmente distribuído como mostrado. Pde-se: (a) Determinar os valores de e , correspondente ao equilíbrio; (b) Sabendo-se que , determinar a mínima espessura que pode ser usada.

Neste caso, como a viga esta apoiada no chão então não há forças de reação locais e sim uma força distribuída sobre toda a sua extensão. Podemos calcular essa forma da forma:

Então a gente sabe que a força total aplicada pela fundação na barra vale , mas além disso é uma carga linearmente distribuída então precisamos achar e . Aplicando o conceito de força concentrada para cargas linearmente distribuídas vamos ter:

Show de bola, agora precisamos de mais uma equação. Essa outra equação será fornecida por meio do somatório dos momentos:

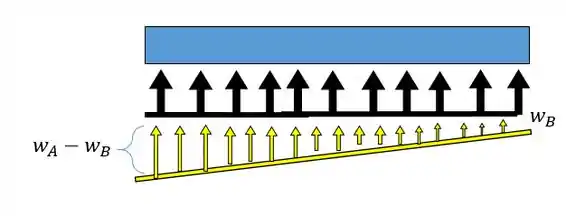
Mas antes de continuar a gente tem que saber a posição onde a força distribuída é aplicada, para isso vamos substituir o nosso carregamento trapezoidal por dois carregamentos, um uniforme e outro triangular da seguinte forma:

O carregamento uniforme terá valor concentrado de:

E atuará exatamente na metade da barra:

Já o carregamento triangular terá valor de:

E atuará no ponto:

Voltando à nossa equação:

Aqui vamos considerar o sentido horário positivo.

Substituindo os valores que achamos:

simplificando por 0,24:

Juntando com a primeira equação temos o nosso sistema:

Substraindo o segundo pelo primeiro:

Resolvida a letra A!

Agora vamos ter que achar o valor do momento fletor máximo, que ocorre exatamente no ponto de aplicação da força de . Para isso vamos aplicar a equação deste carregamento e achar o valor do carregamento em :

Podemos substituis os valores:

Beleza esse é o nosso carregamento, para achar a força cortante a gente integra isso:

Lembrando que o último termo é igual a 11 caso e nulo caso .

do momento fletor.

Agora vamos ter que achar de fato o momento fletor nesse ponto. Para isso vamos achar a equação de momento fletor integrando a da força cortante:

nesse caso não existe momento puro logo assim:

Subsitituindo

Podemos utilizar apenas o módulo:

Agora vamos achar o momento resistente mínimo que a viga deve possuir , que é dado por:

Agora vamos calcular o módulo resistente da barra:

Como

e

Igualando ao valor que achamos: