Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 177b

Para a barra curva e o carregamento mostrado, determinar o percentual de erro introduzido no cálculo da tensão máxima, assumindo-se que a barra é reta. Considerar o caso quando:

  1. r = 5   m m
  2. r = 25   m m
  3. r = 150   m m

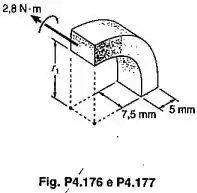
Passo 1

Pra começar, vamos considerar uma viga reta e calcular a tensão sobre ela:

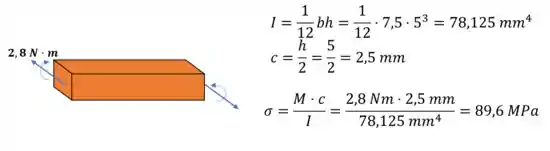
A tensão de tração e de compressão são numericamente iguais a σ = 89,6   M P a

Passo 2

Agora, seguindo os mesmos procedimentos detalhados no Problema 176, vamos calcular a tensão sobre a viga curva.

Pra começar, vamos determinar o raio externo da viga:

r 1 = 2 5   m m

r 2 = r 1 + h = 30   m m

E também já podemos calcular a área de seção transversal

A = h b = 5 ⋅ 7,5 = 37,5   m m 2

O raio do centroide também já pode ser calculado

r - = r 1 + h 2 = 2 5 + 5 2 = 2 7,5   m m

Como a seção é quadrada, o raio da linha neutra pode ser calculado:

R = h ln ⁡ r 2 r 1 = 5 ln ⁡ 3 0   m m 25   m m = 2 7 , 42   m m

E agora podemos calcular a excentricidade entre o centroide e a linha neutra:

e = r - - R = 2 7,5 - 2 7 , 42 = 0 , 08   m m

Passo 3

Tudo certo! Agora é calcular as tensões.

Para região inferior da viga

σ 1 = M r 1 - R A e r 1

σ 1 = - 2,8   N m ⋅ 2 5   m m - 2 7 , 4 2   m m 37,5   m m 2 ⋅ 0 , 08   m m ⋅ 2 5   m m

σ 1 = 9 5,36   M P a

a região superior da viga está sobre compressão:

σ 2 = M r 2 - R A e r 2

σ 2 = - 2,8   N m ⋅ 3 0   m m - 2 7 , 4 2   m m 37,5   m m 2 ⋅ 0 , 08   m m ⋅ 3 0   m m

σ 2 = - 72,62   M P a

Passo 4

Na região de tração o erro é:

E r r o t r a ç ã o = 1 - σ 1 σ = 1 - 9 5,36 89,6 = 6,42 %

E na região de compressão:

E r r o c o m p r e s s ã o = 1 - σ 2 σ = 1 - - 84,44 - 89,6 = 5,7 6 %

Resposta

E r r o t r a ç ã o = 6,42 %

E r r o c o m p r e s s ã o = 5,76 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga-cmxao está sujeita a um momento fletor M = 25 kN · m direcionado, como mostra a figura. Determine a tensão de flexão máxima na viga e a orientação do eixo neutro.
Determine o valor máximo do momento fletor M de modo que a tensão de flexão no elemento não ultrapasse 100M P a .
O momento interno resultante que age na seção transversal da escora de alumínio tem valor M = 520N · m e está direcionado como mostra a figura. Determine a tensão de flexão máxima na escora. A localiz
A viga tem seção transversal retangular. Se estiver sujeita a um momento fletor M=3.500N . m direcionado como mostra a figura, determine a tensão de flexão máxima na viga e a orientação do eixo neutro
Se o momento interno resultante que age na seção transversal da escora de alumínio tiver valor M = 520 N.m e for direcionado como mostra a figura, determine a tensão de flexão nos pontos A e B. A loca