Selecione no apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é e atenção de cisalhamento admissível é
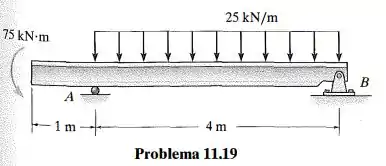
Passo 1
Começamos calculando as reações de apoio

Passo 2
Vamos usar a tabela 6.1 para gerar o diagrama de esforço cortante e momento fletor pelo método gráfico
- : Nessa região não há forças, então o diagrama marca zero.
- : Nessa região há a força localizada positiva que causa um aumento repentino no diagrma. Depois a carga distribuída causa uma queda contínua no gráfico até que atinja o valor de . Então causa um aumento repentino no diagrama.
- : Nessa região não há um momento anti-horário localizado sobre a viga, o que causa uma queda repentina no ponto de aplicação deste momento. O digrama então se mantém constante.
- : Nessa região o gráfico de esforço cortante é positivo, o que causa um aumento no momento fletor correspondente à área abaixo do gráfico do esforço cortante (área azul). Observe que a curva de cortante é decrescente, e isso indica que a curva do momento fletor tem concavidade para baixo.
- Nessa região o gráfico de esforço cortante é negativo, o que causa uma queda no momento fletor correspondente à área abaixo do gráfico do esforço cortante (área laranja). Nessa região o gráfico do esforço cortante é decrescente e isso indica que a curva do momento fletor tem concavidade para baixo.

Para facilitar o cálculo do gráfico de momento fletor, vamos descobrir em que ponto o esforço cortante é zero. Este ponto ocorrerá quando a carga distribuída for igual a reação em A
Com o diagrama de esforço cortante, podemos utilizar novamente a Tabela 6.1 para construir o diagrama de momento fletor.

Passo 3
Agora vamos testar a resistência da viga sobre flexão com a equação 11.1:
Agora podemos olhar o apêndice B e selecionar uma viga apropriada:
Passo 4
Agora vamos testar a resistência da viga ao cisalhamento. Como a viga é de abas largas podemos usar a equação
Como a tensão admissível é de , isso mostra que a viga consegue resistir aos esforços.