Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 116

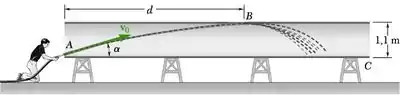
Um trabalhador usa água sob alta pressão para limpar o interior de uma longa canalização de drenagem. Se a água é descarregada com uma velocidade inicial v0 de 11,5 m/s, determine (a) a distância d ao ponto mais remoto B no alto do cano que a água pode lavar a partir de sua posição em A e (b) o ângulo correspondente.

Passo 1

Primeira nota

v x 0 = v 0 cos ⁡ α = 11.5   m/s cos ⁡ α

v y 0 = v 0 sin ⁡ α = 11.5   m/s sin ⁡ α

Por observação, dmax ocorre quando

y max = 1.1   m

Passo 2

Movimento vertical. (Movimento uniformemente acelerado)

v y = v y 0 - g t             y = 0 + v y 0 t - 1 2 g t 2

= 15 sin ⁡ α t - g t             = 11.5 sin ⁡ α t - 1 2 g t 2

Quando

y = y max             e m             B ,             v y B = 0

Então

v y B = 0 = 11.5 sin ⁡ α - g t

t B = 11.5 sin ⁡ α g             g = 9.81   m/ s 2

y B = 11.5 sin ⁡ α t B - 1 2 g t B 2

Passo 3

Substituindo tb e observando yb = 1,1 m

1.1 = 11.5 sin ⁡ α 11.5 sin ⁡ α g - 1 2 g 11.5 sin ⁡ α g 2

= 1 2 g 11.5 2 sin 2   α

sin 2   α = 2.2 × 9.81 11.5 2             α = 23.8265 °

Passo 4

  1. Movimento horizontal. (Uniforme)

x = 0 + v x 0 t = 11.5 cos ⁡ α t

No Ponto B:

x = d max             e             t = t B

onde

t B = 11.5 9.81 sin ⁡ 23.8265 ° = 0.47356   s

Então

d max = 11.5 cos ⁡ 23.8265 ° 0.47356

Resposta

a )   d max = 4.98   m

b )   De cima

α = 23.8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um vagão do metrô parte da estação A e ganha velocidade à razão de 2 m / s ² ² por 6 s e, depois, à razão de 3 m / s ² ² até alcançar a velocidade de 24 m / s . O carro mantém a velocidade até aproxim
O recorde de aceleração mostrado foi obtido para um pequeno avião viajando em um curso reto. Sabendo que x = 0 e v = 60m / s quando t = 0 , determine (a) a velocidade e a posição do avião em t = 20s ,
Conforme mostrado na figura, de t = 0 a t = 4 s , a aceleração de uma dada partícula é representada por uma parábola. Sabendo que x = 0 e v = 8 m / s quando t = 0 , (a) construa as curvas v- -t e x- -
Dois satélites A e B percorrerem órbitas circulares coplanares em torno da Terra com altitudes de 190 e 320 km, respectivamente. Se em t = 0 os satélites estão alinhados como mostrado na figura e sabe
Considere uma partícula de massa m cujo movimento inicia a partir do repouso em um campo gravitacional constante. Se uma força resistiva proporcional ao quadrado da velocidade (isto é, k m v 2 ) for e