Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 131
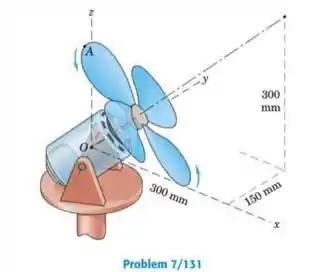
O ventilador elétrico possui uma velocidade constante de no sentido indicado com seu eixo orientado conforme mostrado. Se as componentes e da velocidade do ponto A na extremidade da pá são e , respectivamente, determine o modulo da velocidade da extremidade da pá e o diâmetro das pás do ventilador.
Passo 1
Vamos resolver esse problema nos baseando no ponto A, a velocidade angular e a velocidade linear nesse ponto são perpendiculares, o que significa que o produto interno entre eles é zero:
Com isso podemos obter a última componente da velocidade linear, já que as outras duas já são dadas no enunciado, para calcularmos .
Passo 2
Calculando primeiro o vetor , podemos escrevê-lo como sendo o produto do vetor posição (nas componentes x, y e z) do ponto A vezes a magnitude , dividido pelo módulo do vetor posição:
Passo 3
E o vetor será:
Passo 4
Fazendo o produto interno:
E por fim, calculamos o módulo de
Passo 5
E por fim, calculamos o módulo de
Passo 6
Como o diâmetro é duas vezes o raio do centro até a extremidade A, podemos escrever: