Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 139
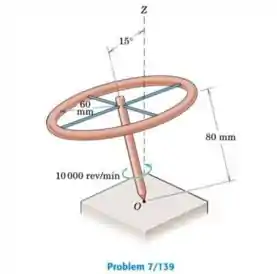
Um pião constituído por um anel de massa e raio médio é montado em um eixo central pontiagudo com raios de massa desprezível. O pião recebe uma velocidade de giro de e é liberado sobre a superfície horizontal com o ponto permanecendo em uma posição fixa. Observa-se o eixo do pião fazer um ângulo de com a vertical enquanto realize precessão. Determine o número N de ciclos de precessão por minuto. Identifique também o sentido da precessão e esboce os cones do corpo e espacial.
Passo 1
Bom, podemos suar a equação para a velocidade angular que representa a precessão do pião, sob ação somente da gravidade:
Passo 2
Vamos agora determinar cada uma das grandezas envolvidas nesse calculo, como o eixo central não possui massa considerável, a posição do centro de massa será a mesma que o centro do anel
O k, podemos obter através de :
E precisamos converter o valor de p para :
Passo 3
Então é:
Portanto, terá sentido anti-horário.
E fazemos o número de ciclos por minutos é:
Passo 4
O cone físico é muito pequeno para valores pequenos de , portanto o cone espacial será:
