Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 7
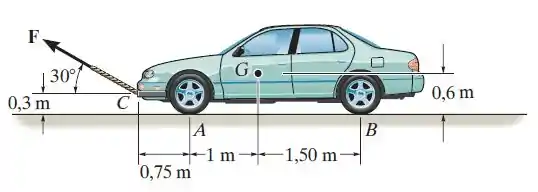
O automóvel tem massa de 2Mg e centro de massa em . Determine a força de reboque exigida para mover o carro se os freios traseiros estão acionados e as rodas dianteiras estão livres para rodar. Considere .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos calcular a força exigida para mover o carro quando os freios traseiros estão acionados e as rodas dianteiras estão livres para rodar.
Bom, para questões como esta, nosso ponto de partir é esboçar um simples diagrama de corpo livre (para facilidade de desenho, vamos transformar o carro em um retângulo). Então, vejamos abaixo o nosso diagrama:
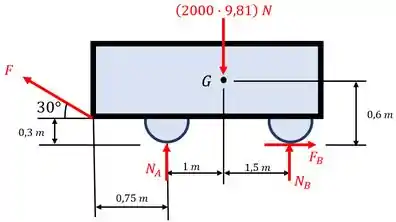
Antes de partirmos para o cálculo, vamos terminar de destrinchar o enunciado da questão. Como os freios traseiros estão acionados, então a força para o qual o carro está na iminência de se mover é:
Já como as rodas dianteiras estão livres para rodar, elas não possuem atrito.
Bom, agora que a gente já sabe todas as relações, vamos para as contas!
Passo 2
Antes que a gente possa descobrir quem é a força , precisamos descobrir qual o valor das forças normais em e em .
E isto é bem simples. Basta esquecermos que existe a força e a força de atrito e aplicarmos as equações.
É exatamente o que devemos fazer depois, só que sem as forças e . Sendo assim, temos:
Portanto, do sistema acima nós obtemos:
Passo 3
Agora é só aplicarmos as equações de equilíbrio considerando a força e a força de atrito . Sendo assim, temos:
Como , então,
Já a força será:
E assim finalizamos a questão!