Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 73
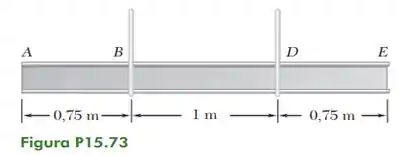
A viga AE de está sendo baixada por dois guindastes. No instante mostrado na figura, sabe-se que a velocidade do ponto D é de para baixo e que a velocidade do ponto E é de para baixo. Determine (a) o centro instantâneo de rotação da viga, (b) a velocidade do ponto A.
Passo 1
Questão 73 agora, meus chapas!
Bom! Pra começar, vamos tentar entender o que mais ou menos está acontecendo em nosso problema...
Se liga! A questão nos diz que os pontos e , tem velocidade para baixo... Ou seja, a viga gira no sentido horário.
Se isso acontece, o ponto também vai ter velocidade para baixo... De modo que o centro de rotação vai estar em algum lugar entre os pontos e , como retratado na figura abaixo...
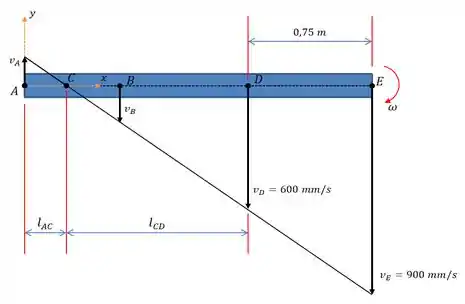
Passo 2
a) Bom! A velocidade angular da barra é dada por...
Sendo assim, podemos obter o valor da distância entre e (), como...
E ao olhar a barra, podemos obter o centro instantâneo de rotação da viga, que é a distância entre e . Ela vai ser dada por...
Passo 3
b) Quanto à velocidade do ponto , basta usar a relação abaixo...
E pronto! Terminamos aqui!
Resposta
a)
b)