Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 5
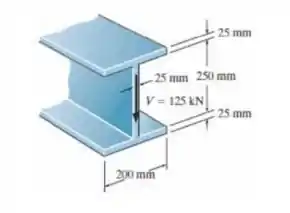
Se a viga de abas largas for submetida a um cisalhamento V = 125 kN, determine a força de cisalhamento à qual a alma da viga resistirá.
Passo 1
Falaaa galerinha do RespondeAí, tudo belezinha?
Saca só, nesse exercício aqui o enunciado nos diz que a viga de abas largas está submetida a um cisalhamento , sabendo disso ele nos pede para determinar a força de cisalhamento à qual a alma da viga resistirá.
Belezoca, então pra gente resolver essa questão devemos obter a tensão cisalhante em função de e depois distribuir pela área da alma. Bora lá ver como fica essa brincadeira!
Passo 2
Começamos calculando o momento de inércia da seção transversal (pra variar haha):
Lembrando que o momento de inércia para um retângulo é calculado como:
Se tivermos de utilizar o princípio dos eixos paralelos (como vamos fazer para as abas superior e inferior):
Show, então nosso momento de inércia vai ser dado por:
Passo 3
E depois o momento estático em função de y lembrando que o momento estático é calculado como:
Aqui, vamos dividir essa viga em duas, e vamos olhar apenas para a metade superior dela.
Vamos fazer para os dois componentes mais escuros e repare que a área do retângulo que está em pé, varia com o valor de y.
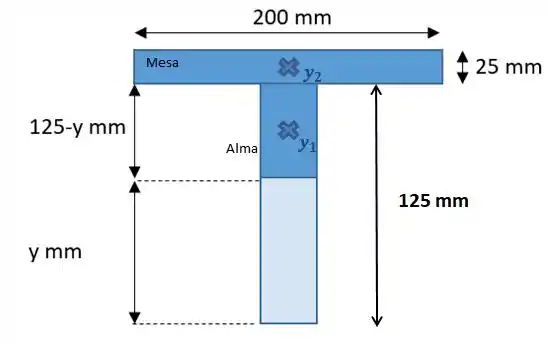
Calculando essas áreas e os pontos (passando tudo para metros), vamos ter:
Passo 4
Temos agora tudo que precisamos para calcular o cisalhamento em função de y, basta substituir na equação do cisalhamento:
Passo 5
E, então, distribuímos pela área da alma, integrando:
Aqui o nosso limite de integração para a variável vai ser de -0,125 até 0,125, pois quando calculamos o nosso y, consideramos a metade da nossa viga, sendo assim, y vai da base da alma () até o topo ()!