Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 12

Determine, com aproximação de múltiplos de 5 mm, a largura mínima da viga que suportará com segurança a carga P = 40 k N . A tensão de flexão admissível é σ a d m = 168   M P a e a tensão de cisalhamento admissível é τ a d m = 105   M P a

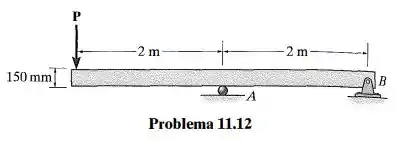
Passo 1

Começamos calculando as reações de apoio

∑ M B = 0 ⇒ P ⋅ 4 - R A ⋅ 2 = 0

R A = 80   k N

∑ F Y = 0 ⇒ - P + R A - R B = 0

R B = 40   k N

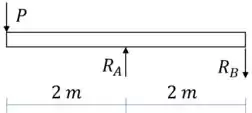
Passo 2

Utilizamos o método gráfico para gerar o diagrama de esforço cortante e momento fletor:

V m a x = 40   k N

M m a x = 80   k N ⋅ m

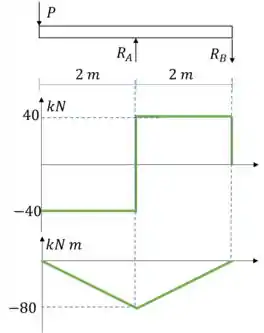
Passo 3

Vamos calcular as propriedades geométricas da seção:

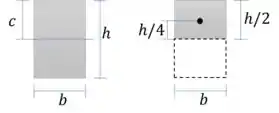
Momento de inércia:

I = 1 12 b h 3

Aplicação do momento:

c = h 2

Momento estático

Q = h 2 ⋅ b ⋅ h 4

Q = b h 2 8

Passo 4

Vamos testar a resistência sobre flexão:

σ = M c I

Se considerarmos que a seção é quadrada, podemos substituir o momento de inércia e a distância de aplicação:

σ = M ⋅ ( h / 2 ) 1 12 b h 3

Isolando a base:

b = 6 M σ ⋅ h 2

Aplicando os valores:

b = 6 ⋅ 80   k N ⋅ m 168   M P a ⋅ 150   m m 2

b = 6 ⋅ 80   k N ⋅ m 168   M P a ⋅ 150   m m 2

b = 126,98   m m

Arredondando:

b = 130   m m

Passo 5

Agora vamos testar a viga quanto ao cisalhamento:

τ = V Q I t

Expandindo:

τ = V ⋅ b h 2 8 1 12 b h 3 ⋅ b

Simplificando:

τ = 1,5 V b h

Aplicamos os valores:

105   M P a = 1,5 ⋅ 40   k N 150   m m ⋅ b

O valor da base é:

b = 3,08   m m

Passo 6

Para garantir a resistência, escolhemos as maiores dimensões

b = 130   m m

Resposta

b = 130   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no meio do vão: (a) a maior tensão normal; (b) a maior tensão de cisalhame
Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (a) a maior tensão normal; (b) a tensão de cisalhamento no ponto a ; (c) a maior tensão de cisalhamento.
Três tábuas, cada uma com seção transversal retangular de 40 x 90 mm, são pregadas juntas para formar uma viga que é submetida a uma força cortante vertical de 1,1 kN. Sabendo-se que o espaçamento ent
Resolva o Prob. 5.2, considerando que o espaçamento entra os pregos é aumentado para s = 100 mm
Três tábuas, cada uma com 50 mm de espessura, são pregadas juntas para formar uma viga que é submetida a uma força cortante vertical. Sabendo-se que a força de cisalhamento admissível em cada prego é